CBSE 12TH MATHEMATICS - Online Test
Q1. If l, m and n are direction cosines of the position vector OP the coordinates of P are
Answer : Option A
Explaination / Solution:
If l , m and n are the direction cosines of vector denoted by , then , the coordinates of point P are given by : lr ,mr and nr respectively.
Q2. An instructor has a question bank consisting of 300 easy True / False questions,200 difficult True / False questions, 500 easy multiple choice questions and 400 difficult multiple choice questions. If a question is selected at random from the question bank, what is the probability that it will be an easy question given that it is a multiple choice question?
Answer : Option E
Explaination / Solution:
| True/False | MCQ |
Easy | 300 | 500
|
Difficult | 200 | 400 |
Total = 1400, therefore n(S) = 1400 Let A = event of getting easy question B = event of getting multiple choice question.
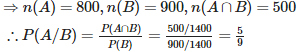
Q3. If then the value of is
Answer : Option B
Explaination / Solution:
Q4. is equal to
Answer : Option B
Explaination / Solution:
limx→π2[sinx]=0[sinceπ2−h≤x≤π2+h]
Q5. limx→01−cosxx2 is equal to
Answer : Option A
Explaination / Solution:
(UsingL’hospital Rule ).
Q6. The degree of the equationis
Answer : Option B
Explaination / Solution:
the power of the highest order derivative i.e . is 2.hence the degree 2
Q7. Skew lines are lines in different planes which are
Answer : Option B
Explaination / Solution:
By definition : The Skew lines are lines in different planes which are neither parallel nor intersecting .
Q8. The area lying in the first quadrant and bounded by the curve y = , the x – axis and the ordinates at x = - 2 and x = 1 is
Answer : Option D
Explaination / Solution:
Required area :
Q9. If then A is
Answer : Option A
Explaination / Solution:
A square matrix A for which, where n is a positive integer, is called a Nilpotent matrix.
The determinant and trace of the matrix is always Zero for a Nilpotent Matrix.
For the given matrix "A", determinant (A)=0 and trace(A)=0.
Q10. The function f (x) = – 2 x is increasing in the interval
Answer : Option A
Explaination / Solution:
f(x) = x2- 2x
f'(x) = 2x - 2 = 2(x - 1)
So , f( x) is increasing if 2(x-1) 0 , i.e.if x 1
f'(x) = 2x - 2 = 2(x - 1)
So , f( x) is increasing if 2(x-1) 0 , i.e.if x 1
