Three Dimensional Geometry - Online Test
Q1. Direction cosines of a line are
Answer : Option D
Explaination / Solution:
a line when intersect another line or axis two kind of angle form ,as an assumption we take positive side of axis, to define the direction of line we take angle made from all three axis.and we take cos not other trigonometric function like sin,tan because we can define Direction cosines of a line are coefficient of i,j,k of a unit vector along that line.
Q2. If l, m, n are the direction cosines of a line, then
Answer : Option D
Explaination / Solution:
we know that direction cosines is coefficient of i,j,k of unit vector along that line ,i.e those coefficient are l,m,n .the length of the line r is such that and magnitute of unit vector r is 1 and . on squaring both side we get
Q3.
is a vector joining two points P(x1, y1, z1) and Q(x2, y2, z2).If ,Direction cosines of are
Answer : Option A
Explaination / Solution:
since we know Direction cosines of a line are coefficient of i,j,k of a unit vector along that line,first find a vector then to convert it unit vector divide by its magnitute || the coefficient of this unit vector will be
Q4. If l, m and n are the direction cosines of a line, Direction ratios of the line are the numbers which are
Answer : Option C
Explaination / Solution:
If l, m and n are the direction cosines of a line, Direction ratios of the line are the numbers which are Proportional to the direction cosines of the line.
Q5. If l, m, n are the direction cosines and a, b, c are the direction ratios of a line then
Answer : Option D
Explaination / Solution:
using direction ratio a,b,c we got a vector along the line ,for direction cosine find unit vector then 
where l,m,n represent direction cosine
where l,m,n represent direction cosine
Q6. Skew lines are lines in different planes which are
Answer : Option B
Explaination / Solution:
By definition : The Skew lines are lines in different planes which are neither parallel nor intersecting .
Q7. Angle between skew lines is
Answer : Option A
Explaination / Solution:
Angle between skew lines is the angle between two intersecting lines drawn from any point parallel to each of the skew lines .
Q8. If and are the direction cosines of two lines; and is the acute angle between the two lines; then
Answer : Option A
Explaination / Solution:
If and are the direction cosines of two lines; and is the acute angle between the two lines; then the cosine of the angle between these two lines is given by : .
Q9. If and are the direction ratios of two lines and is the acute angle between the two lines; then
Answer : Option A
Explaination / Solution:
If and are the direction ratios of two lines and is the acute angle between the two lines; then , the cosine of the angle between these two lines is given by :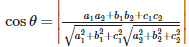 
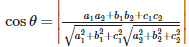
Q10. Vector equation of a line that passes through the given point whose position vector is and parallel to a given vector is
Answer : Option A
Explaination / Solution:
Vector equation of a line that passes through the given point whose position vector is and parallel to a given vector is given by : 
