Probability - Online Test
Q1. A coin is tossed three times, if E : head on third toss , F : heads on first two tosses. Find P(E|F)
Answer : Option B
Explaination / Solution:


Q2. A coin is tossed three times, E : at most two tails , F : at least one tail. Find P(E|F)
Answer : Option C
Explaination / Solution:
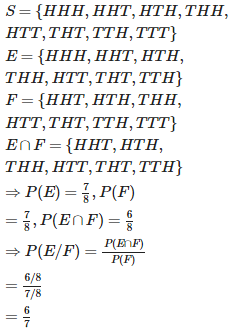
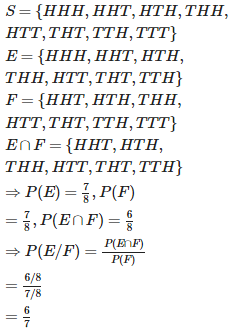
Q3. A black and a red dice are rolled. Find the conditional probability of obtaining a sum greater than 9, given that the black die resulted in a 5.
Answer : Option C
Explaination / Solution:
n(S)=36.
Let A = event of getting sum greater than 9.
= {(4,6),(5,5),(6,4),(5,6),(6,5),(6,6)}
And B = event of getting 5 on black die.
={(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)}
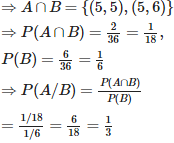
Let A = event of getting sum greater than 9.
= {(4,6),(5,5),(6,4),(5,6),(6,5),(6,6)}
And B = event of getting 5 on black die.
={(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)}
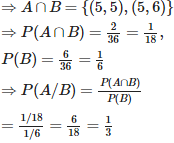
Q4. A black and a red dice are rolled. Find the conditional probability of obtaining the sum 8, given that the red die resulted in a number less than 4.
Answer : Option A
Explaination / Solution:


Q5. An instructor has a question bank consisting of 300 easy True / False questions,200 difficult True / False questions, 500 easy multiple choice questions and 400 difficult multiple choice questions. If a question is selected at random from the question bank, what is the probability that it will be an easy question given that it is a multiple choice question?
Answer : Option E
Explaination / Solution:
| True/False | MCQ |
Easy | 300 | 500
|
Difficult | 200 | 400 |
Total = 1400, therefore n(S) = 1400 Let A = event of getting easy question B = event of getting multiple choice question.
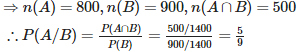
Q6. Consider the experiment of throwing a die, if a multiple of 3 comes up, throw the die again and if any other number comes, toss a coin. Find the conditional probability of the event ‘the coin shows a tail’, given that ‘at least one die shows a 3’.
Answer : Option C
Explaination / Solution:
S = {(3,1), (3,2), (3,3), (3,4), (3,5), (3,6), (6,1), (6,2), (6,3), (6,4), (6,5), (6,6), (1,H), (2,H), (4,H), (5,H), (1,T), (2,T), (4,T), (5,T)} Let A = event that coin shows a tail. i.e. A = { (1,T), (2,T), (4,T), (5,T)} and B = event that atleast one die shows 3. B = {(3,1), (3,2), (3,3), (3,4), (3,5), (3,6),(6,3)}
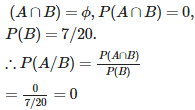
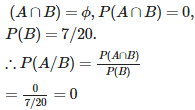
Q7. If P(A) = , P(B) = 0, then P(A|B) is
Answer : Option D
Explaination / Solution:
We know that :
which is not defined
which is not defined
Q8. If A and B are events such that P(A|B) = P(B|A), then
Answer : Option B
Explaination / Solution:
It is given that :
Q9. If E and F are independent, then
Answer : Option A
Explaination / Solution:
we know that
If E and F are independent, then P(E/F) = P(E) and P(F/E) = P(F)
P (E ∩ F) = P (E) P (F).
Q10. If E and F are independent, then
Answer : Option A
Explaination / Solution:
If E and F are independent, then P (E|F) = P (E), P (F) ≠ 0 .
