Three Dimensional Geometry - Online Test
Q1.
Equation of a line through a point and having direction cosines l, m, n is
Answer : Option A
Explaination / Solution:
Equation of a line through a point (x1, y1, z1) and having direction cosines l, m, n is given by :
Q2. Vector equation of a line that passes through two points whose position vectors are 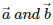 is
is
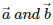 is
is
Answer : Option D
Explaination / Solution:
Vector equation of a line that passes through two points whose position vectors are 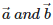 is given by:
is given by: 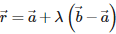
 is given by:
is given by: 
Q3.
Cartesian equation of a line that passes through two points and is
Answer : Option C
Explaination / Solution:
Cartesian equation of a line that passes through two points and is given by : .
Q4.
If is the acute angle between , then
Answer : Option C
Explaination / Solution:
If is the acute angle between , then cosine of the angle between these two lines is given by : 
Q5. Shortest distance between two skew lines is
Answer : Option B
Explaination / Solution:
Shortest distance between two skew lines is The line segment perpendicular to both the lines .
Q6. Shortest distance between is
Answer : Option A
Explaination / Solution:
Shortest distance between
is given by :
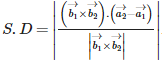
is given by :
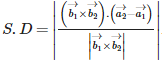
Q7.
Shortest distance between the lines and is
Answer : Option B
Explaination / Solution:
Shortest distance between the lines and is given by: 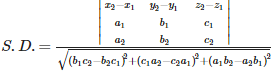
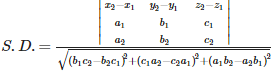
Q8.
If a line makes angles with the x, y and z – axes respectively, find its direction cosines.
Answer : Option D
Explaination / Solution:
If a line makes angles with the x, y and z – axes respectively, then the direction cosines of this line is given by :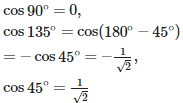
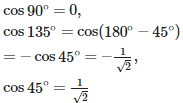
Q9. If a line has the direction ratios – 18, 12, – 4, then what are its direction cosines ?
Answer : Option A
Explaination / Solution:
If a line has the direction ratios – 18, 12, – 4, then its direction cosines are given by:


Q10.
Find the equation of the line which passes through the point (1, 2, 3) and is parallel to the vector.
Answer : Option D
Explaination / Solution:
The equation of the line which passes through the point (1, 2, 3) and is parallel to the vector
, let vector and vector ,
the equation of line is :
.
, let vector and vector ,
the equation of line is :
.
