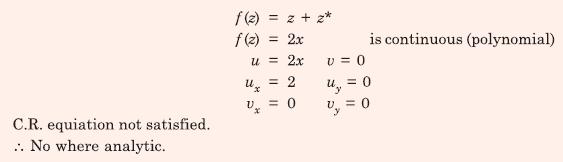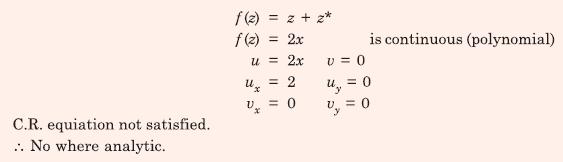Signals and Systems - Online Test
Q1. For linear time invariant systems, that are Bounded Input Bounded stable, which one of the following statement is TRUE?
Answer : Option B
Explaination / Solution:
No Explaination.
Q2. Consider a signal defined by
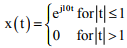
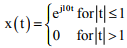
Its Fourier Transform is
Answer : Option A
Explaination / Solution:
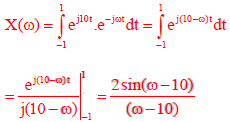
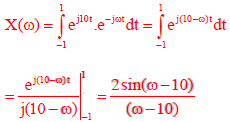
Q3. The following discrete-time equations result from the numerical integration of the differential equations of an un-damped simple harmonic oscillator with state variables x and y. The integration time step is h.
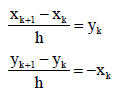
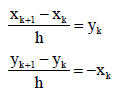
For this discrete-time system, which one of the following statements is TRUE?
Answer : Option A
Explaination / Solution:
No Explaination.
Q4. A function y(t), such that y(0) = 1 and y(1) = 3e-1, is a solution of the differential equation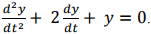 
Then y(2) is
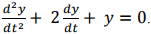Then y(2) is
Answer : Option B
Explaination / Solution:
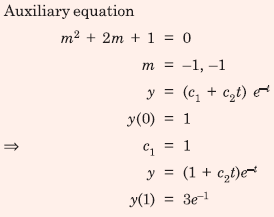
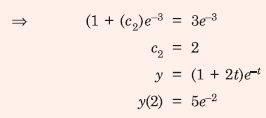
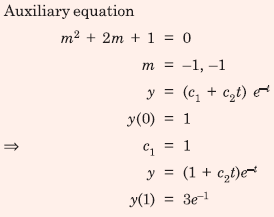
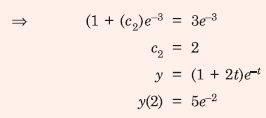
Q5. The value of the integral
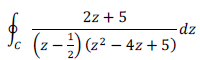
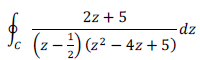
over the contour |z| = 1, taken in the anti-clockwise direction, would be
Answer : Option B
Explaination / Solution:
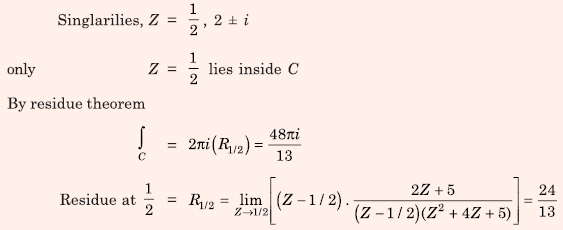
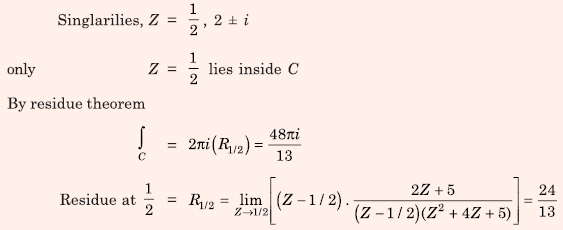
Q6. Consider a continuous-time system with input x(t) and output y(t) given by
y(t) = x(t) cos(t)
This system is
Answer : Option C
Explaination / Solution:
Q7. Suppose x1(t) and x2(t) have the Fourier transforms as shown below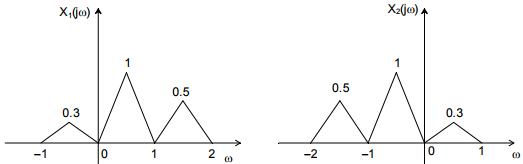
Which one of the following statements is TRUE?
Answer : Option C
Explaination / Solution:
Q8. The output of a continuous-time, linear time-invariant system is denoted by T{x(t)} where x(t) is
the input signal. A signal z(t) is called eigen-signal of the system T , when T{z(t)} = γz(t),
where γ is a complex number, in general, and is called an eigenvalue of T. Suppose the impulse
response of the system T is real and even. Which of the following statements is TRUE?
Answer : Option D
Explaination / Solution:
Q9. Consider a causal LTI system characterized by differential equation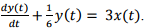 
The response of the system to the input 
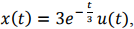where u(t) denotes the unit step
function, is
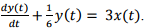The response of the system to the input 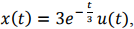where u(t) denotes the unit step
function, is
Answer : Option D
Explaination / Solution:
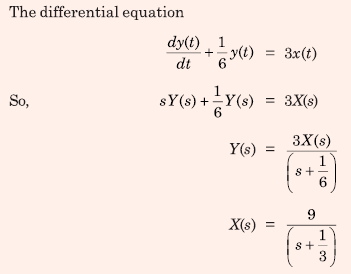
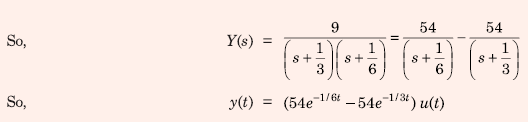
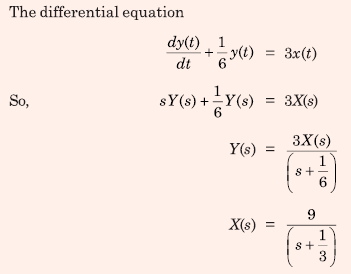
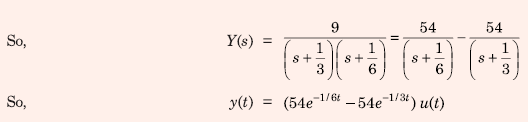
Q10. Consider the function ݂f(z) = z + z* where z is a complex variable and z* denotes its complex
conjugate. Which one of the following is TRUE?
Answer : Option B
Explaination / Solution:
