Gravitation - Online Test
The area A swept out by a planet of mass m in time interval t is related to the angular momentum by:
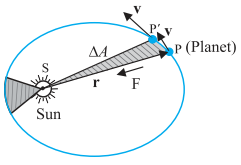
The law of areas can be understood as the consequence of conservation of angular momentum which is valid for any central for A central force is such that the force on the planet is along the vector joining the sun and the planet. Let the sun be at the origin and let the position and momentum of the planet be denoted by r and p respectively. Then the area swept out by the planet of mass m in the time interval Δt is given by ΔA = ½ (r × vΔt).
Hence ΔA/Δt =½ (r × p)/m, (since v=p/m)
= L / (2 m)
where v is the velocity, where v is the velocity, L is the angular
momentum equal to ( r × p ). For a central force, which is directed along r, L is a constant
Newton’s law of universal gravitation states that the gravitational force of attraction between any two particles of masses m1 and m2 separated by a distance r has the magnitude
since gravitational force is attractive in nature, so if there are two particles of m1 & m2 .
So One Force will be on m1 which will be directed towards m 2. i.e
And other force wiil be on m2 which will be directed towards m 1 i.e
Clearly, It can be seen that Because thsese forces are attracted to each other and direction of each force is opposite to other one.
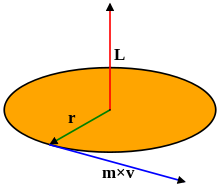
The motion of a particle under a central force F always remains in the plane defined by its initial position and velocity.This may be seen by symmetry. Since the position r, velocity v and force F all lie in the same plane, there is never an acceleration perpendicular to that plane, because that would break the symmetry between "above" the plane and "below" the plane.
To demonstrate this mathematically, it suffices to show that the angular momentum of the particle is constant. This angular momentum L is defined by the equation
The gravitational force on point mass m1 due to point mass m2, m3 & m4 is:
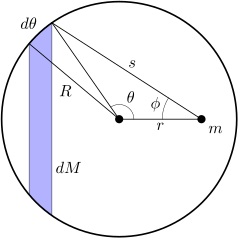
According to Shell's theorem, If a particle of mass m is located outside a spherical shell of mass M at, for instance, point P, the shell attracts the particle as though the mass of the shell were concentrated at its centre. Thus, as far as the gravitational force acting on a particle outside the shell is concerned, a spherical shell acts no differently from the solid spherical distributions of mass.
