Gravitation Online Objective Test | Gravitation Online Objective Test

# Gravitation # CBSE 11TH PHYSICS Prepare / Learn

Q1. The force of attraction due to a hollow spherical shell of uniform density, on a point mass situated inside it, is

A. positive

B. zero

C. negative

D. none of these

Answer : Option B
Explaination / Solution:

The gravitational force acting by a spherically symmetric shell upon a point mass inside it, is the vector sum of gravitational forces acted by each part of the shell, and this vector sum is equal to zero. That is, a mass m within a spherically symmetric shell of mass M will feel no net force

# Gravitation # CBSE 11TH PHYSICS Prepare / Learn

Q2. In Cavendish’s experiment,

A. net force on bar AB having two small lead spheres due to gravitational forces is negative

B. net torque on bar AB having two small lead spheres due to gravitational forces is positive

C. net force on bar AB having two small lead spheres due to gravitational forces is positive

D. torque on bar AB having two small lead spheres due to gravitational forces is balanced by the restoring torque of the wire

Answer : Option D
Explaination / Solution:

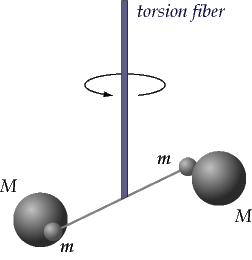
Cavendish's apparatus for experimentally determining the value of G involved a light, rigid rod about 2-feet long. Two small lead spheres were attached to the ends of the rod and the rod was suspended by a thin wire. When the rod becomes twisted, the torsion of the wire begins to exert a torsional force that is proportional to the angle of rotation of the rod. The more twist of the wire, the more the system pushes backwards to restore itself towards the original position.

# Gravitation # CBSE 11TH PHYSICS Prepare / Learn

Q3. The value of the gravitational constant G is

A. G = 6.67

\times

1 0^{- 11}

N m/kg

^{2}

B. G = 6.67

\times

1 0^{- 11}

N m

^{2}

/kg

C. G = 6.67

\times

1 0^{- 11}

^{2}

/kg

^{2}

D. G = 6.67

\times

1 0^{- 11}

N m

^{2}

/kg

^{2}

Answer : Option D
Explaination / Solution:

The value of G was experimentally determined by Lord Henry Cavendish using a torsion balance.Cavendish brought two large lead spheres near the smaller spheres attached to the rod. Since all masses attract, the large spheres exerted a gravitational force upon the smaller spheres and twisted the rod a measurable amount. Once the torsional force balanced the gravitational force, the rod and spheres came to rest and Cavendish was able to determine the gravitational force of attraction between the masses.Cavendish expressed his result in terms of the density of the Earth.

$G = g \frac{R_{e a r t h}^{2}}{M_{e a r t h}} = \frac{3 g}{4 π R_{e a r t h} ρ_{e a r t h}}$

After converting to SI units, Cavendish's value for the Earth's density, 5.448 g cm−3, gives

G = 6.74×10−11 m3 kg–1 s−2

Today, the currently accepted value is 6.67259 x 10-11 N m2/kg2.

# Gravitation # CBSE 11TH PHYSICS Prepare / Learn

Q4. The acceleration due to gravity at a height h in terms of mass of earth

M_{E}

and radius of the earth

R_{E}

and gravitational constant G is

A. g(h)=ME(RE+h)2

g(h)=GmME(RE+h)2

C.

g(h)=GME(RE+2h)2

D. g(h)=ME(RE+h)2

Answer : Option A
Explaination / Solution:

We know by Newton's law of gravitation, the force on the body of mass m, situated at height h to the surface of the earth of mass ME is given by:

$F = G \frac{M_{e} m}{{(r + h)}^{2}}$ -(1)

we also know F=mass X acceleration( here acceleration is acceleration due to gravity)

$\Rightarrow$ F=mg -(2)

Equating (i) & (ii), we get

$g = G \frac{M_{e}}{{(r + h)}^{2}}$

# Gravitation # CBSE 11TH PHYSICS Prepare / Learn

Q5. The acceleration due to gravity at a depth d in terms of g the acceleration due to gravity at radius of the earth

R_{E}

A. g(d)=g(1−2dRE)

B. g(d)=g(1+dRE)

C. g(d)=g(1+d2RE)

D. g(d)=g(1−dRE)

Answer : Option D
Explaination / Solution:

Acceleration due to gravity at the surface of the earth of radius RE

$g = G \frac{M}{R_{E}^{2}} = \frac{4}{3} π ρ G R_{E}$ -(1)

Acceleration due to gravity at depth d from the surface of the earth

$g (d) = \frac{4}{3} π ρ G (R - d)$ -(2)

From (1) & (2), we get

$g (d) = g (1 - \frac{d}{R_{E}})$

# Gravitation # CBSE 11TH PHYSICS Prepare / Learn

Q6. Escape speed from the earth is the

A. minimum speed at which to throw an object such that it does not fall back to the earth

B. none of these

C. minimum speed at which to throw an object such that it falls back to the earth

D. maximum speed at which to throw an object such that it does not fall back to the earth

Answer : Option A
Explaination / Solution:

The escape velocity is the minimum velocity required to leave a planet or moon. For a rocket or other object to leave a planet, it must overcome the pull of gravity.

$V_{e s c a p e} = \sqrt{\frac{2 G M}{R}}$

Vescape=11184 m/sec approximate to 11.2 km/sec

# Gravitation # CBSE 11TH PHYSICS Prepare / Learn

Q7. For earth satellites, the centripetal force is provided by

A. forces exerted by firing rockets on satellite

B. strong interactions

C. electrical forces

D. gravitational force

Answer : Option D
Explaination / Solution:

Gravity supplies the necessary centripetal force to hold a satellite in orbit about the earth. Setting the gravity force from the universal law of gravity equal to the required centripetal force yields the equation of motion of satellites in the circular orbit

i.e $F_{g r a v i t y} = F_{c e n t r i p e t a l}$

$\Rightarrow v_{o r b i t a l} = \sqrt{\frac{G M}{r}}$

# Gravitation # CBSE 11TH PHYSICS Prepare / Learn

Q8. The total energy of a circularly orbiting satellite is

A. positive small

B. zero

C. positive large

D. negative

Answer : Option D
Explaination / Solution:

When a satellite revolves around a planet in its orbit, it possesses both potential energy (due to its position against the gravitational pull of earth) and kinetic energy (due to orbital motion).

$∴ \begin{matrix} Total Energy = Potential Energy(U) + Kinetic Energy(K) \\ = \frac{- G M m}{r} + \frac{G M m}{2 r} \\ = \frac{- G M m}{2 r} = \frac{- L^{2}}{2 m r^{2}} \end{matrix}$

Hence we can say that total energy of circularly orbiting satellite is negative.

# Gravitation # CBSE 11TH PHYSICS Prepare / Learn

Q9. For a circularly orbiting satellite the potential energy

A. is negative, and has a magnitude twice that of the positive kinetic energy.

B. is negative, and having a magnitude twice that of the negative kinetic energy.

C. is negative, and having a magnitude twice that of the positive kinetic energy.

D. is negative, and has a magnitude thrice that of the positive kinetic energy.

Answer : Option A
Explaination / Solution:

In case of circularly orbiting satellite,

$\begin{matrix} Potential Energy = \frac{- G M m}{r} = \frac{- L^{2}}{m r^{2}} \\ KineticEnergy = \frac{- G M m}{2 r} = \frac{L^{2}}{2 m r^{2}} \end{matrix}$

Comparing both, we can say that the potential energy is negative and has a magnitude twice that of the positive kinetic energy.

# Gravitation # CBSE 11TH PHYSICS Prepare / Learn

Q10. For Geostationary Satellites

A. circular orbit is in the equatorial plane of the earth and period of rotation is 14 hrs

B. circular orbit is in the equatorial plane of the earth and period of rotation is 34 hrs

C. circular orbit is in the equatorial plane of the earth and period of rotation is 24 hrs

D. circular orbit is in the longitudinal plane of the earth and period of rotation is 20 hrs

Answer : Option C
Explaination / Solution:

If there is a satellite in the equatorial plane rotating in the direction of earth’s rotation from west to east, then for an observer, on the earth, angular velocity of satellite will be $(ω_{s} - ω_{E})$

The time interval between the two consecutive appearances overhead will be,

$T = \frac{2 π}{ω_{s} - ω_{E}} = \frac{T_{s} T_{E}}{T_{E} - T_{s}}$

If $ω_{s} = ω_{E}, T = \infty$ , i.e. satellite will appear stationary relative to earth. Such satellites are called geostationary satellites and will have a period of rotation as the period of rotation of earth i.e 24 Hrs.

Gravitation - Online Test

Gravitation | Online Objective Test | Start Test

Prepare Before Start Test | Learn

UPSC Civil services Entrance exams | Online Test

GATE Exam | Online Test

Under Graduate Entrance Exams | Online Test

Problem Solving and Reasoning | Online Test

CAT Entrance Exams | Online Test

CLAT LAW Entrance exams | Online Test

Banking Entrance exams | Online Test

UGC NET Entrance exams | Online Test

TANCET Anna University | Online Test

TN State Board | Online Test