Engineering Mathematics - Online Test
Q1. An analytic function of a complex variable z = x + iy is expressed as f(z) = w(x, y) + iv(x, y),
where i = √−1. If u(x, y) = x2 – y2, then expression for v(x, y) in terms of x, y and a general
constant c would be
Answer : Option C
Explaination / Solution:
Given f(z) = w(x, y) + iv(x, y), is analytic and x = x2 - y2
We know that if f(z) = µ+iv is analytic then C-R equations will be satisfied.
∂µ/∂x = ∂v/∂xy and ∂µ/∂y = -∂v/∂x
v = 2xy + c is correct answer
Q2. Consider two solutions x(t) = x1(t) and x(t) and x(t) = x2(t) of the differential equation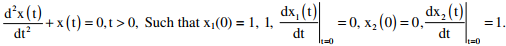 
The Wronskian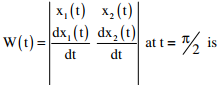 
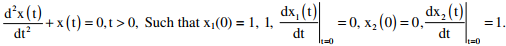The Wronskian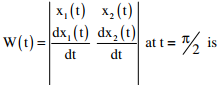
Answer : Option A
Explaination / Solution:
Given Differential equation is
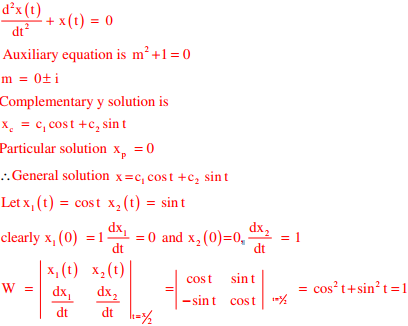
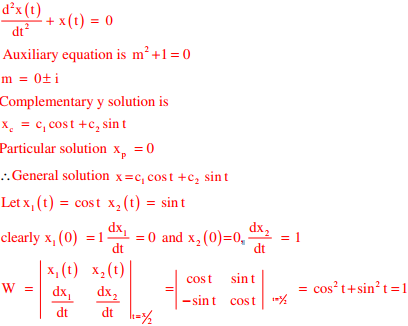
Q3. A series expansion for the function sinθ is
Answer : Option B
Explaination / Solution:
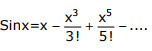
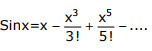
Q4. What is 
equal to?
equal to?
Answer : Option D
Explaination / Solution:
Applying L’ Hospitals rule, we have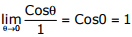 
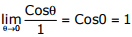
Q5. Eigen values of a real symmetric matrix are always
Answer : Option C
Explaination / Solution:
Eigen values of a real symmetric matrix are always real
Q6. The product of two complex numbers 1 + i and 2-5i is
Answer : Option A
Explaination / Solution:
(1 + i)(2 -5i) = 2 - 5i + 2i + 5 = 7 - 3i
Q7. If f(x) is an even function and a is a positive real number, then 
equals
equals
Answer : Option D
Explaination / Solution:
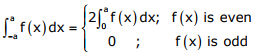
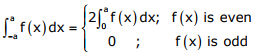
Q8. The integral 
when evaluated by using Simpson’s 1/3 rule on two equal
subintervals each of length 1, equals
when evaluated by using Simpson’s 1/3 rule on two equal
subintervals each of length 1, equals
Answer : Option C
Explaination / Solution:
Q9. Consider the differential equation 
. The general solution with
constant c is
. The general solution with
constant c is
Answer : Option D
Explaination / Solution:
No Explaination.
Q10. An unbiased coin is tossed five times. The outcome of each toss is either a head
or a tail. The probability of getting at least one head is
Answer : Option D
Explaination / Solution:
P(at least one head) = 1- P (no heads) = 1 - (1/25) = 31/32
