Engineering Mathematics - Online Test
Q1. Roots of the algebraic equation x3 + x2 + x + 1 = 0 are
Answer : Option D
Explaination / Solution:
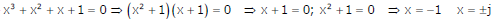
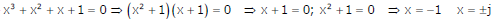
Q2. With K as a constant, the possible solution for the first order differential equation 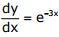 is
is
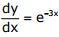 is
is
Answer : Option A
Explaination / Solution:
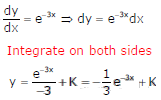
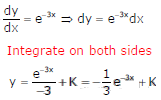
Q3. The function f(x) = 2x - x2 - x3 + 3 has
Answer : Option C
Explaination / Solution:
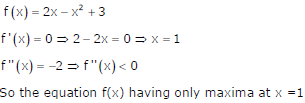
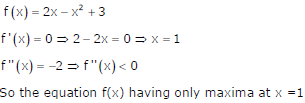
Q4. The matrix 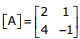 is decomposed into a product of a lower triangular
matrix [L] and an upper triangular matrix [U]. The properly decomposed [L] and
[U] matrices respectively are
is decomposed into a product of a lower triangular
matrix [L] and an upper triangular matrix [U]. The properly decomposed [L] and
[U] matrices respectively are
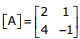 is decomposed into a product of a lower triangular
matrix [L] and an upper triangular matrix [U]. The properly decomposed [L] and
[U] matrices respectively are
is decomposed into a product of a lower triangular
matrix [L] and an upper triangular matrix [U]. The properly decomposed [L] and
[U] matrices respectively are
Answer : Option D
Explaination / Solution:
[A] = [L][U] Option D is correct
Q5. The two vectors [1,1,1] and [1, a, a2], where a = 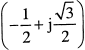 , are
, are
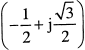 , are
, are
Answer : Option B
Explaination / Solution:
Dot product of two vectors = 1 + a + a2 = 0
So orthogonal
Q6. Two independent random variables X and Y are uniformly distributed in the interval [–1,1]. The probability that max[X, Y] is less than 1/2 is
Answer : Option B
Explaination / Solution:
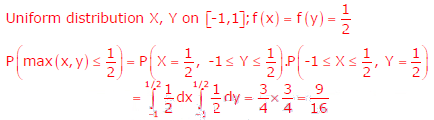
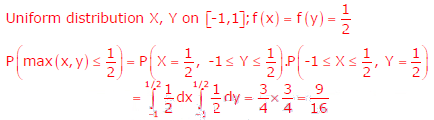
Q7. If 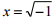 , then the value of xx is
, then the value of xx is
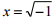 , then the value of xx is
, then the value of xx is
Answer : Option A
Explaination / Solution:
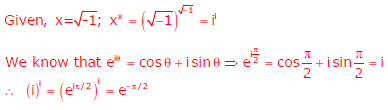
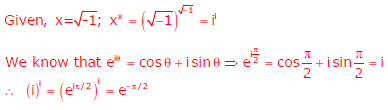
Q8. With initial condition
x(1) = 0.5, the solution of the differential equation 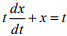 is
is
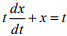 is
is
Answer : Option D
Explaination / Solution:
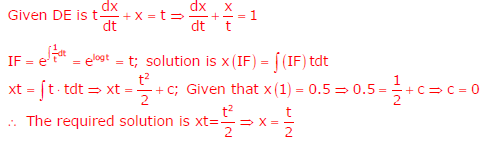
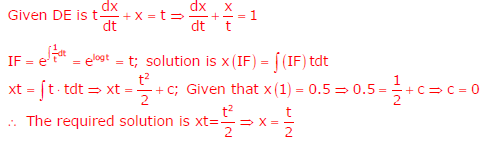
Q9. The maximum value of F(x) = x3 – 9x2 + 24x + 5 in the interval [1, 6] is
Answer : Option C
Explaination / Solution:
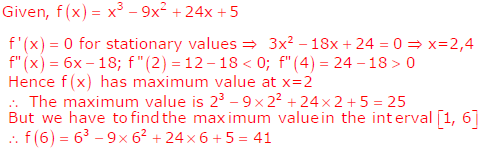
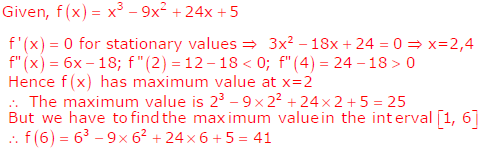
Q10. 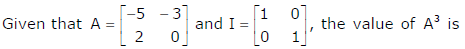
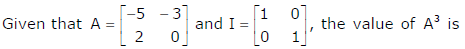
Answer : Option B
Explaination / Solution:


