Digital Logic - Online Test
Q1. What is the minimum number of gates required to implement the Boolean function (AB + C) if we have to use only 2-input NOR gates?
Answer : Option B
Explaination / Solution:
No Explaination.
Q2. The minterm expansion of f 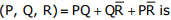
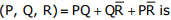
Answer : Option A
Explaination / Solution:
No Explaination.
Q3. P is a 16-bit signed integer. The 2’s complement representation of P is (F87B)16.
The 2’s complement representation of 8*P is
Answer : Option A
Explaination / Solution:
No Explaination.
Q4. 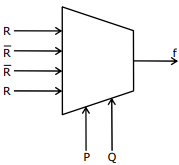
The Boolean expression for the output f of the multiplexer shown below is

Answer : Option A
Explaination / Solution:
No Explaination.
Q5. The simplified SOP (Sum of Product) form of the Boolean expression
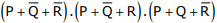 is
is
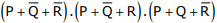 is
is
Answer : Option B
Explaination / Solution:
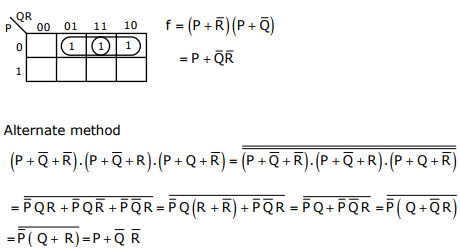
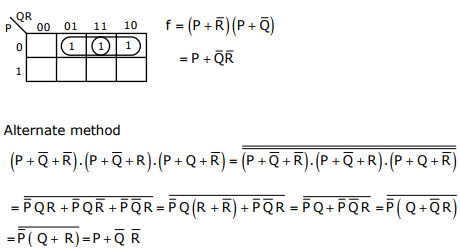
Q6. Which one of the following circuits is NOT equivalent to a 2-input XNOR
(exclusive NOR) gate?
Answer : Option D
Explaination / Solution:
All options except option ‘D’ gives EX-NOR gates
Q7. The minimum number of D flip-flops needed to design a mod-258 counter is
Answer : Option A
Explaination / Solution:
2n ≥ 258 ⇒ n = 9
Q8. Consider the following circuit involving three D-type flip-flops used in a certain
type of counter configuration.
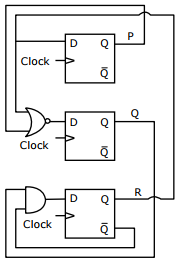

If all the flip-flops were reset to 0 at power on, what is the total number of
distinct outputs (states) represented by PQR generated by the counter?
Answer : Option C
Explaination / Solution:
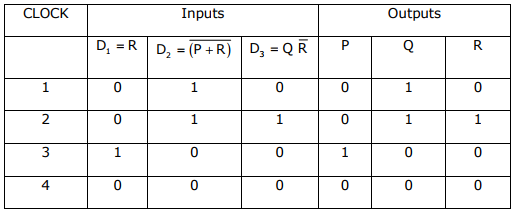

So Total number of distinct outputs is 4
Q9. Consider the following circuit involving three D-type flip-flops used in a certain type of counter configuration.


If at some instance prior to the occurrence of the clock edge, P. Q and R have a
value 0, 1 and 0 respectively, what shall be the value of PQR after the clock
edge?
Answer : Option D
Explaination / Solution:
From the Table Shown in the explanation of question 50, if first state is 010 next
State is 011
Q10. The decimal value 0.5 in IEEE single precision floating point representation has
Answer : Option B
Explaination / Solution:
(0.5)10 = (1.0)2 × 2-1
So, exponent = -1 and fraction is 000 - - - 000