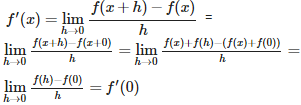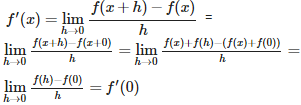Continuity and Differentiability - Online Test
Q1. If both f and g are defined in a nhd of 0 ; f(0) = 0 = g(0) and f ‘ (0) = 8 = g’ (0), then is equal to
Answer : Option A
Explaination / Solution:
( by using L’Hospital Rule )
Q2. The derivative of f(x) = | x | at x = 0 is
Answer : Option B
Explaination / Solution:
which does not exist at x = 0 .
Q3. If x + | y | = 2y , then y as a function of x is
Answer : Option C
Explaination / Solution:
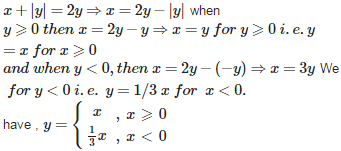
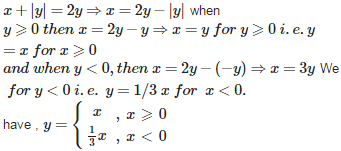
Q4. Let f(x) = | x−1|, then
Answer : Option A
Explaination / Solution:
here f(x)=|x−1| x∈R. So f(x) is not derivable when x−1=0 i.e. at x=1
Q5. If f(x) = then
Answer : Option C
Explaination / Solution:
therefore , f is neither continuous nor differentiable at x = 0
Q6. In case of strict increasing functions, slope of the tangent and hence derivative is
Answer : Option D
Explaination / Solution:
If f is strictly increasing function , then f ‘ (x) can be 0 also . For example , f(x) = x3 is strictly increasing , but its derivative is 0 at x = 0. As another example , take f(x) = x + cosx ; here f ‘(x) = 1 – sinx , which is either +ve or 0 and the function x + cos x is strictly increasing.
Q7. Let f(x) = x – [x], then f ‘ (x) = 1 for
Answer : Option B
Explaination / Solution:
f(x) = x - is derivable at all x R – I , and f ‘(x) = 1 for all x R – I
Q8.
Let f (x + y) = f(x) + f(y) x, y Suppose that f (6) = 5 and f ‘ (0) = 1, then f ‘ (6) is equal to
Answer : Option B
Explaination / Solution:
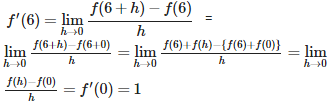
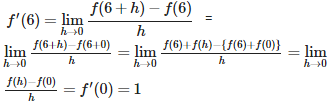
Q9.
If x sin (a + y) = sin y, then is equal to
Answer : Option C
Explaination / Solution:
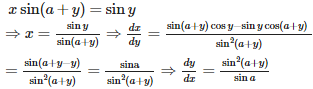
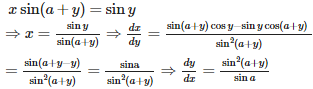
Q10. Let f be a function satisfying f(x + y) = f(x) + f(y) for all x, y then f ‘ (x) =
Answer : Option B
Explaination / Solution: