Continuity and Differentiability - Online Test
Q1. is equal to
Answer : Option B
Explaination / Solution:
( using L’Hospital Rule)
Q2.
is equal to
Answer : Option B
Explaination / Solution:
limx→0tanxlog(1+x)=limx→0tanxxxlog(1+x)=limx→0tanxx.limx→011xlog(1+x)=1.11=1
Q3. The function f (x) = 1 + | sin x l is
Answer : Option D
Explaination / Solution:
is not derivable at those x for which is continuous everywhere (being the sum of two continuous functions)
Q4. The function, f (x) = (x – a) sin for x a and f (a) = 0 is
Answer : Option D
Explaination / Solution:
Q5. Let f (x) = [x], then f (x) is
Answer : Option A
Explaination / Solution:
f(x) = [x] is derivable at all x except at integral points i.e. on R – I .
Q6. The function f (x) = [x] is
Answer : Option D
Explaination / Solution:
Case 1 Let c be a real number which is not equal to any integer. for all real numbers close to c the value of the function is equal to [c]; i.e., . Also and hence the function is continuous at all real numbers not equal to integers.
Case 2 Let c be an integer. Then we can find a sufficiently small real number such that
This, in terms of limits mean that
Since these limits cannot be equal to each other for any c, the function is discontinuous at every integral point.
Q7. If f (x) is a polynomial of degree m (⩾1) , then which of the following is not true ?
Answer : Option D
Explaination / Solution:
As all the three remaining statements are true for the given function.
Q8. If f(x) = x | x | ∀x∈R, then
Answer : Option B
Explaination / Solution:
Also, f'(x)
,
Therefore f'(x) exists at all
Further, f'(0) =
Q9. 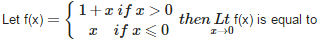
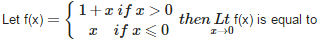
Answer : Option D
Explaination / Solution:
Does not exist.
Q10. If f (x) = (1 – x) tan , then f(x) is equal to
Answer : Option A
Explaination / Solution:
