Chapter 7: Applications of Differential Calculus - Online Test
Q1.
The volume of a sphere is increasing in volume at the rate of 3π
cm3 / sec .
Answer : Option A
Explaination / Solution:


Q2. A balloon rises straight up at 10 m/s. An
observer is 40 m away from the spot
where the balloon left the ground. The rate of change of the balloon’s angle of
elevation in radian per second when the balloon is 30 metres above the ground.
Answer : Option B
Explaination / Solution:
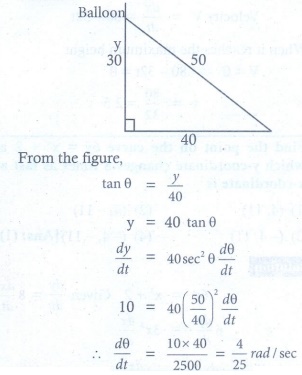
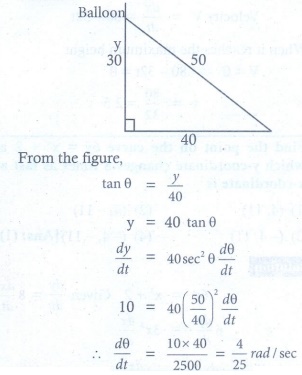
Q3. The position of a particle moving along a
horizontal line of any time t is
given by s (t) = 3t2 − 2t − 8 . The time at which the particle is at rest is
Answer : Option B
Explaination / Solution:
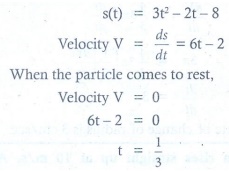
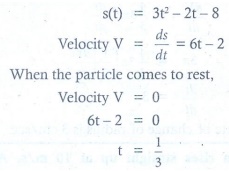
Q4. A stone is thrown up vertically. The height it
reaches at time t seconds is given by x =
80t −16t2 . The stone reaches the maximum height in time t seconds is given by
Answer : Option B
Explaination / Solution:
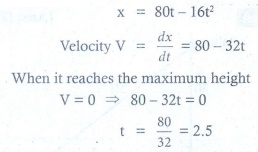
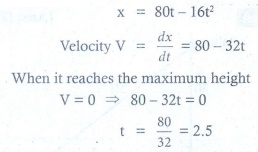
Q5. The point on the curve 6y = x3 + 2 at which y-coordinate changes 8 times as fast
as x-coordinate is
Answer : Option A
Explaination / Solution:
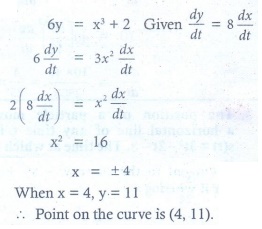
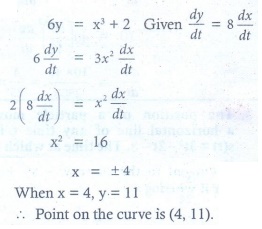
Q6. The abscissa of the point on the curve f (x) = √(8−2x) at which the slope of
the tangent is −0.25 ?
Answer : Option B
Explaination / Solution:


Q7. The slope of the line normal to the curve f (x) = 2 cos 4x at x = π/12 is
Answer : Option C
Explaination / Solution:


Q8. The tangent to the curve y2 − xy + 9 =
0 is vertical when
Answer : Option D
Explaination / Solution:


Q9. Angle between
y2 = x and x2 = y at the origin is
Answer : Option C
Explaination / Solution:


Q10. The value of the limit 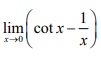 is
is
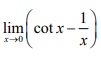 is
is
Answer : Option A
Explaination / Solution:


