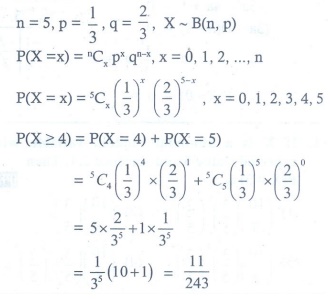Chapter 11: Probability Distributions - Online Test
Q1.
Let x be random
variable with probability density function
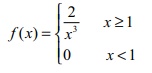
Answer : Option B
Explaination / Solution:


Q2.
A rod of length 2l
is broken into two pieces at random. The probability density function of the
shorter of the two pieces is
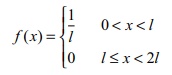
The mean and variance of the shorter of the two pieces are respectively
Answer : Option D
Explaination / Solution:
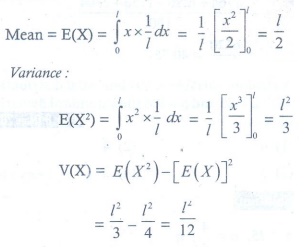
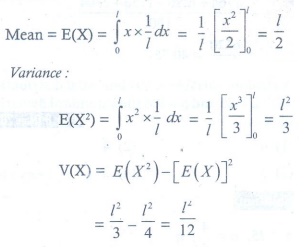
Q3. Consider a game where the player tosses a
six-sided fair die. If the face that comes up is 6, the player wins ₹ 36, otherwise he loses ₹ k 2
, where k is the face that comes up k
= {1, 2, 3, 4, 5}. The expected amount to win at this game in ₹ is
Answer : Option B
Explaination / Solution:


Q4. A pair of dice numbered 1, 2, 3, 4, 5, 6 of a
six-sided die and 1, 2, 3, 4 of a four-sided die is rolled and the sum is
determined. Let the random variable X
denote this sum. Then the number of elements in the inverse image of 7 is
Answer : Option D
Explaination / Solution:
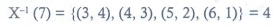
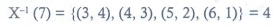
Q5. A random variable X has binomial distribution with n = 25 and p = 0.8 then
standard deviation of X is
Answer : Option D
Explaination / Solution:
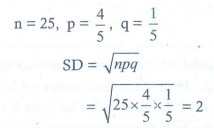
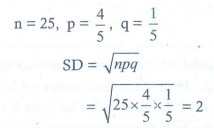
Q6. Let X
represent the difference between the number of heads and the number of tails
obtained when a coin is tossed n
times. Then the possible values of X are
Answer : Option B
Explaination / Solution:
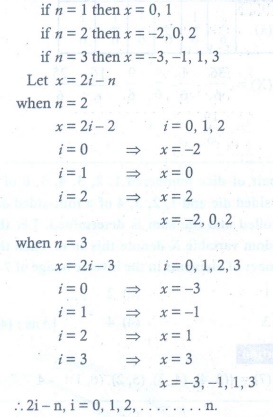
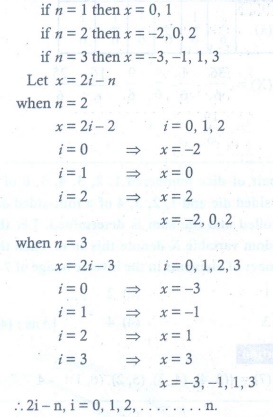
Q7. If the function f (x) = 1/12 for a < x < b , represents
a probability density function of a continuous random variable X, then which of the following cannot be
the value of a and b?
Answer : Option D
Explaination / Solution:
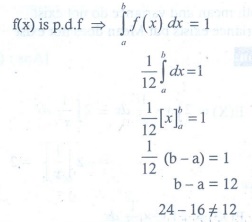
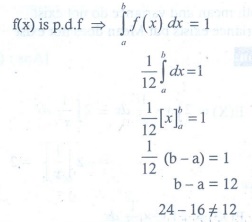
Q8.
Four buses carrying 160 students from the same school arrive
at a football stadium. The buses carry, respectively, 42, 36, 34, and 48
students. One of the students is randomly selected. Let X denote the number of students that were on the bus carrying the
randomly selected student. One of the
4 bus drivers is also randomly selected. Let Y denote the number of students on that bus.
Answer : Option C
Explaination / Solution:


Q9. Two coins are to be flipped. The first coin will
land on heads with probability 0.6, the second with Probability 0.5. Assume
that the results of the flips are independent, and let X equal the total number of heads that result. The value of E(X)
is
Answer : Option B
Explaination / Solution:


Q10. On a multiple-choice exam with 3 possible
destructives for each of the 5 questions, the probability that a student will
get 4 or more correct answers just by guessing is
Answer : Option A
Explaination / Solution: