Basic Numeracy - Online Test
Q1. From a group of 7 men and 6 women, five persons are to be selected to form a committee so that at least 3 men are there on the committee. In how many ways can it be done?
Answer : Option D
Explaination / Solution:
We may have (3 men and 2 women) or (4 men and 1 woman) or (5 men only).
 Required number of ways | = (7C3 x 6C2) + (7C4 x 6C1) + (7C5) | |||||||||||
| ||||||||||||
| ||||||||||||
| = (525 + 210 + 21) | ||||||||||||
| = 756. |
Q2. If one-third of one-fourth of a number is 15, then three-tenth of that number is:
Answer : Option D
Explaination / Solution:
Let the number be x.
| Then, | 1 | of | 1 | of x = 15  x = 15 x 12 = 180. |
| 3 | 4 |
| So, required number = |  | 3 | x 180 |  | = 54. |
| 10 |
Q3. What decimal of an hour is a second ?
Answer : Option C
Explaination / Solution:
| Required decimal = | 1 | = | 1 | = .00027 |
| 60 x 60 | 3600 |
Q4. The cube root of .000216 is:
Answer : Option B
Explaination / Solution:
| (.000216)1/3 | = | | 216 | | 1/3 |
| 106 |
| = | | 6 x 6 x 6 | | 1/3 |
| 102 x 102 x 102 |
| = | 6 |
| 102 |
| = | 6 |
| 100 |
= 0.06
Q5. Two numbers are respectively 20% and 50% more than a third number. The ratio of the two numbers is:
Answer : Option C
Explaination / Solution:
Let the third number be x.
| Then, first number = 120% of x = | 120x | = | 6x |
| 100 | 5 |
| Second number = 150% of x = | 150x | = | 3x |
| 100 | 2 |
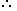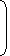| Ratio of first two numbers = | | 6x | : | 3x | | = 12x : 15x = 4 : 5. |
| 5 | 2 |
Q6. Three pipes A, B and C can fill a tank from empty to full in 30 minutes, 20 minutes, and 10 minutes respectively. When the tank is empty, all the three pipes are opened. A, B and C discharge chemical solutions P,Q and R respectively. What is the proportion of the solution R in the liquid in the tank after 3 minutes?
Answer : Option B
Explaination / Solution:
| Part filled by (A + B + C) in 3 minutes = 3 | | 1 | + | 1 | + | 1 | 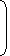| = | | 3 x | 11 | 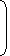| = | 11 | . |
| 30 | 20 | 10 | 60 | 20 |
| Part filled by C in 3 minutes = | 3 | . |
| 10 |
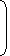| Required ratio = | | 3 | x | 20 | | = | 6 | . |
| 10 | 11 | 11 |
Q7. A vessel is filled with liquid, 3 parts of which are water and 5 parts syrup. How much of the mixture must be drawn off and replaced with water so that the mixture may be half water and half syrup?
Answer : Option C
Explaination / Solution:
Suppose the vessel initially contains 8 litres of liquid.
Let x litres of this liquid be replaced with water.
| Quantity of water in new mixture = | | 3 - | 3x | + x | 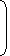| litres |
| 8 |
| Quantity of syrup in new mixture = | | 5 - | 5x | 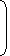| litres |
| 8 |
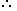| | 3 - | 3x | + x | 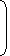| = | | 5 - | 5x | |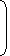
| 8 | 8 |
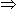5x + 24 = 40 - 5x
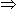10x = 16
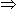| x = | 8 | . |
| 5 |
| So, part of the mixture replaced = | | 8 | x | 1 | 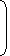| = | 1 | . |
| 5 | 8 | 5 |
Q8. In a 100 m race, A can give B 10 m and C 28 m. In the same race B can give C:
Answer : Option B
Explaination / Solution:
A : B = 100 : 90.
A : C = 100 : 72.
| B : C = | B | x | A | = | 90 | x | 100 | = | 90 | . |
| A | C | 100 | 72 | 72 |
When B runs 90 m, C runs 72 m.
| When B runs 100 m, C runs | | 72 | x 100 | 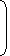m | = 80 m. |
| 90 |
B can give C 20 m.
Q9. Tickets numbered 1 to 20 are mixed up and then a ticket is drawn at random. What is the probability that the ticket drawn has a number which is a multiple of 3 or 5?
Answer : Option D
Explaination / Solution:
Here, S = {1, 2, 3, 4, ...., 19, 20}.
Let E = event of getting a multiple of 3 or 5 = {3, 6 , 9, 12, 15, 18, 5, 10, 20}.
| P(E) = | n(E) | = | 9 | . |
| n(S) | 20 |
Q10. The banker's discount on a bill due 4 months hence at 15% is Rs. 420. The true discount is:
Answer : Option A
Explaination / Solution:
| T.D. |
| |||||||||||
| ||||||||||||
| ||||||||||||
| = Rs. 400. |
