Basic Numeracy - Online Test
| Speed= |  | 60 x | 5 |  m/sec m/sec | = |  | 50 |  m/sec. m/sec. |
| 18 | 3 |
Length of the train = (Speed x Time).
 Length of the train = Length of the train = |  | 50 | x 9 |  m = 150 m. m = 150 m. |
| 3 |
| Speed of the train relative to man = |  | 125 |  m/sec m/sec |
| 10 |
| = |  | 25 |  m/sec. m/sec. |
| 2 |
| = |  | 25 | x | 18 |  km/hr km/hr |
| 2 | 5 |
= 45 km/hr.
Let the speed of the train be x km/hr. Then, relative speed = (x - 5) km/hr.
 x - 5 = 45
x - 5 = 45  x = 50 km/hr.
x = 50 km/hr.
Let AB be the lighthouse and C and D be the positions of the ships.
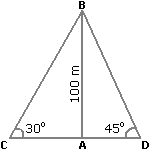
Then, AB = 100 m,  ACB = 30° and
ACB = 30° and  ADB = 45°.
ADB = 45°.
| AB | = tan 30° = | 1 |  AC = AB x √3 = 100√3 m. AC = AB x √3 = 100√3 m. |
| AC | √3 |
| AB | = tan 45° = 1  AD = AB = 100 m. AD = AB = 100 m. |
| AD |
 CD = (AC + AD) CD = (AC + AD) | = (100√3 + 100) m |
| = 100(√3 + 1) | |
| = (100 x 2.73) m | |
| = 273 m. |
Let AB be the wall and BC be the ladder.

Then,  ACB = 60º and AC = 4.6 m.
ACB = 60º and AC = 4.6 m.
| AC | = cos 60º = | 1 |
| BC | 2 |
 BC BC | = 2 x AC |
| = (2 x 4.6) m | |
| = 9.2 m. |
S.I. for 1 year = Rs. (854 - 815) = Rs. 39.
S.I. for 3 years = Rs.(39 x 3) = Rs. 117.
 Principal = Rs. (815 - 117) = Rs. 698.
Principal = Rs. (815 - 117) = Rs. 698.
Let the sum invested in Scheme A be Rs. x and that in Scheme B be Rs. (13900 - x).
| Then, |  | x x 14 x 2 |  | + |  | (13900 - x) x 11 x 2 |  | = 3508 |
| 100 | 100 |
 28x - 22x = 350800 - (13900 x 22)
28x - 22x = 350800 - (13900 x 22)
 6x = 45000
6x = 45000
 x = 7500.
x = 7500.
So, sum invested in Scheme B = Rs. (13900 - 7500) = Rs. 6400.
Let C.P. of each article be Re. 1 C.P. of x articles = Rs. x.
S.P. of x articles = Rs. 20.
Profit = Rs. (20 - x).
 |  | 20 - x | x 100 = 25 |  |
| x |
 2000 - 100x = 25x
2000 - 100x = 25x
125x = 2000
 x = 16.
x = 16.
Let C.P.= Rs. 100. Then, Profit = Rs. 320, S.P. = Rs. 420.
New C.P. = 125% of Rs. 100 = Rs. 125
New S.P. = Rs. 420.
Profit = Rs. (420 - 125) = Rs. 295.
 Required percentage = Required percentage = |  | 295 | x 100 |  % % | = | 1475 | % = 70% (approximately). |
| 420 | 21 |
Let their marks be (x + 9) and x.
| Then, x + 9 = | 56 | (x + 9 + x) |
| 100 |
 25(x + 9) = 14(2x + 9)
25(x + 9) = 14(2x + 9)
 3x = 99
3x = 99
 x = 33
x = 33
So, their marks are 42 and 33.
Suppose originally he had x apples.
Then, (100 - 40)% of x = 420.
 | 60 | x x = 420 |
| 100 |
 x = x = |  | 420 x 100 |  = 700. = 700. |
| 60 |
