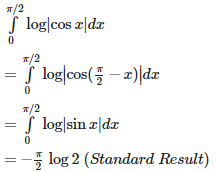CBSE 12TH MATHEMATICS - Online Test
Q1. The value of the determinant 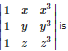
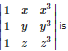
Answer : Option D
Explaination / Solution:
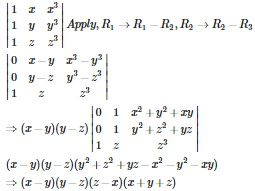
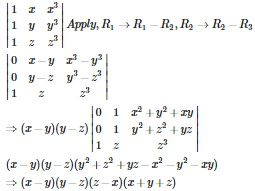
Q2. Let R be the feasible region (convex polygon) for a linear programming problem and let Z = ax + by be the objective function. When Z has an optimal value (maximum or minimum), where the variables x and y are subject to constraints described by linear inequalities,
Answer : Option D
Explaination / Solution:
Let R be the feasible region (convex polygon) for a linear programming problem and let Z = ax + by be the objective function. When Z has an optimal value (maximum or minimum), where the variables x and y are subject to constraints described by linear inequalities then , optimal value must occur at a corner point (vertex) of the feasible region.
Q3. Let A = {a, b, c} and R = {(a, a), (b, b), (c, c), (b, c) } be a relation on A. Here, R is
Answer : Option D
Explaination / Solution:
Any relation R is reflexive if x R x for all x ∈ R. Here ,(a, a), (b, b), (c, c)∈ R. Therefore , R is reflexive.
Q5. Zero Vector
Answer : Option C
Explaination / Solution:
A vector whose initial and terminal points coincides is called Zero Vector. The magnitude of Zero Vector is also Zero.
Q6. Consider the experiment of throwing a die, if a multiple of 3 comes up, throw the die again and if any other number comes, toss a coin. Find the conditional probability of the event ‘the coin shows a tail’, given that ‘at least one die shows a 3’.
Answer : Option C
Explaination / Solution:
S = {(3,1), (3,2), (3,3), (3,4), (3,5), (3,6), (6,1), (6,2), (6,3), (6,4), (6,5), (6,6), (1,H), (2,H), (4,H), (5,H), (1,T), (2,T), (4,T), (5,T)} Let A = event that coin shows a tail. i.e. A = { (1,T), (2,T), (4,T), (5,T)} and B = event that atleast one die shows 3. B = {(3,1), (3,2), (3,3), (3,4), (3,5), (3,6),(6,3)}
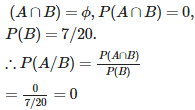
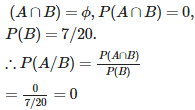
Q7. cos2θ is not equal to
Answer : Option B
Explaination / Solution:
is equals to 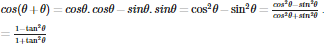
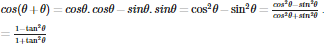
Q8. is equal to
Answer : Option D
Explaination / Solution:
Q9. Find the order and degree of is
Answer : Option A
Explaination / Solution:
Order = 3 ,Since the highest order derivative is but degree cannot be defined ,because the deriative term y’ is present in exponential form.
Q10. Angle between skew lines is
Answer : Option A
Explaination / Solution:
Angle between skew lines is the angle between two intersecting lines drawn from any point parallel to each of the skew lines .