CBSE 12TH MATHEMATICS - Online Test
Q1. If P(A) = , P(B) = and P(A ∪ B) = find P(A|B)
Answer : Option B
Explaination / Solution:
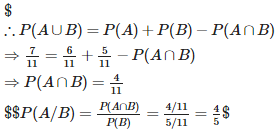
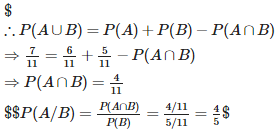
Q2.
is equal to
Answer : Option B
Explaination / Solution:
cot−1x=θ⇒x=cotθ⇒cotθ=x1sin(cot−1x)=sinθ=Perp.Hyp.=1x2+1√.
Q3.
Let f (x + y) = f(x) + f(y) x, y Suppose that f (6) = 5 and f ‘ (0) = 1, then f ‘ (6) is equal to
Answer : Option B
Explaination / Solution:
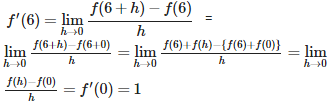
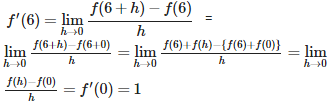
Q4. Find the shortest distance between the lines 

Answer : Option C
Explaination / Solution:
The given equations can be reduced as: 



Q5. If A and B are two non-zero square matrices such that AB = 0, then
Answer : Option D
Explaination / Solution:
The product of two non-zero matrices can be a zero matrix iff one of the two given matrices should be singular.
Q6. Find a particular solution of when
Answer : Option B
Explaination / Solution:
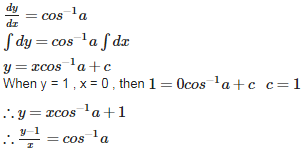
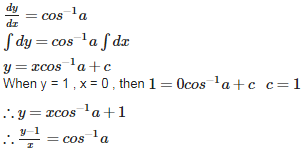
Q7.
The normal to the curve 2 y = 3 – at (1, 1) is
Answer : Option C
Explaination / Solution:
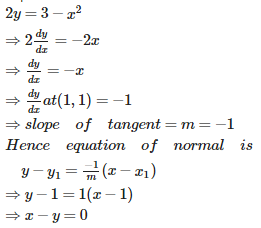
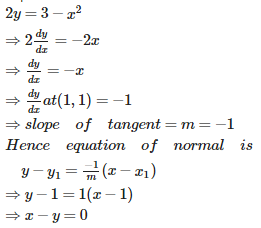
Q8. Minimize Z = x + 2y subject to x + 2y ≥ 100, 2x – y ≤ 0, 2x + y ≤ 200; x, y ≥ 0.
Answer : Option B
Explaination / Solution:
Objective function is Z = x + 2 y ……………………(1).
The given constraints are : x + 2y ≥ 100, 2x – y ≤ 0, 2x + y ≤ 200; x, y ≥ 0.
The corner points are obtained by drawing the lines x+2y=100, 2x-y=0 and 2x+y=200.
The points so obtained are (0,50),(20,40), (50,100) and (0,200)
Corner points | Z = x + 2y |
D(0 ,50 ) | 100……………..(Min.) |
A(20,40) | 100……………………..(Min.) |
B(50,100) | 250 |
C(0,200) | 400 |
Here , Z = 100 is minimum at ( 0, 50) and ( 20 ,40).
Minimum Z = 100 at all the points on the line segment joining the points (0, 50) and (20, 40).
Q9. The area of the smaller segment cut off from the circle by x = 1 is
Answer : Option C
Explaination / Solution:
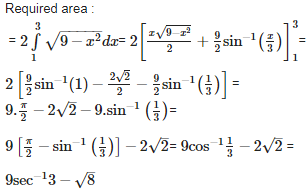
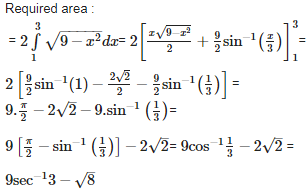
Q10. In Z , the set of integers , inverse of – 7 , w.r.t. ‘ * ‘ defined by a*b = a +b + 7 for all a,b∈Z ,is
Answer : Option B
Explaination / Solution:
If ‘ e ‘ is the identity ,then a*e = a ⇒a + e + 7 = a ⇒ e = - 7 . Also,inverse of e is e itself. Hence , inverse of -7 is -7.
