CBSE 12TH MATHEMATICS - Online Test
Q1. In the figure which are the Equal vectors?
Answer : Option B
Explaination / Solution:
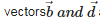are equal vectors , because they have equal magnitude and same direction.
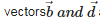are equal vectors , because they have equal magnitude and same direction.
Q2. If P (A) = 0.8, P (B) = 0.5 and P(B|A) = 0.4, find P(A|B)
Answer : Option B
Explaination / Solution:
We have ,
P (A) = 0.8, P (B) = 0.5 and P(B|A) = 0.4
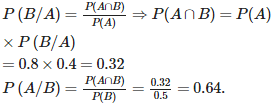
P (A) = 0.8, P (B) = 0.5 and P(B|A) = 0.4
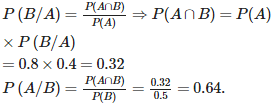
Q3. If then is equal to
Answer : Option C
Explaination / Solution:
sin−1x+cos−1x=π2cos−1x=π2−sin−1x=π2−π5=3π10.
Q4. If f(x) = then
Answer : Option C
Explaination / Solution:
therefore , f is neither continuous nor differentiable at x = 0
Q5. Find the shortest distance between the lines 
Answer : Option D
Explaination / Solution:
Q6. If for a matrix A, where I is the identity matrix, then A equals
Answer : Option D
Explaination / Solution:
Q7. General solution of is
Answer : Option C
Explaination / Solution:
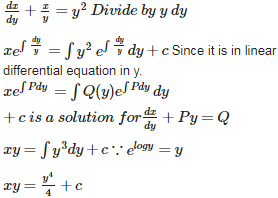
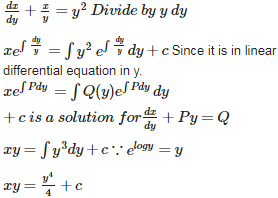
Q8.
The tangent to the parabola at the point makes with the X – axis an angle of
Answer : Option D
Explaination / Solution:
Therefore , slope of tangent at ( 1 , ½ ) = 1. Hence , required angle is
Therefore , slope of tangent at ( 1 , ½ ) = 1. Hence , required angle is
Q9.
The area bounded by the ellipse and the straight line x + 3y = 3 is
Answer : Option A
Explaination / Solution:
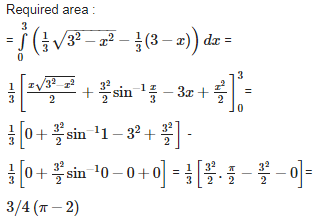
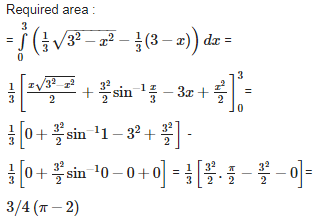
Q10. Maximize Z = 3x + 2y subject to x + 2y ≤ 10, 3x + y ≤ 15, x, y ≥ 0.
Answer : Option A
Explaination / Solution:
Objective function is Z = 3x + 2 y ……………………(1).
The given constraints are : x + 2y ≤ 10, 3x + y ≤ 15, x, y ≥ 0. The corner points obtained by drawing the lines 3x+y=15 and x+2y=10 graphically are (0,0),(0,5), (5,0) and (4,3).
Corner points | Z = 3x + 2y |
O(0 ,0 ) | 0 |
A(5,0) | 15 |
B(0,5) | 10 |
C(4,3) | 18……………………..(Max.) |
Here , Z = 18 is maximum at ( 4, 3 )
