cbse 12th mathematics | Online Objective Test

Linear Programming Prepare / Learn

Q1. Minimise Z = – 3x + 4 y subject to x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0.

A. Minimum Z = – 15 at (5, 1)

B. Minimum Z = – 14 at (5, 0)

C. Minimum Z = – 13 at (4, 1)

D. Minimum Z = – 12 at (4, 0)

Answer : Option D
Explaination / Solution:

Objective function is Z = - 3x + 4 y ……………………(1).
The given constraints are : x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0.

The corner points obtained by constructing the line x+2y=8 and 3x +2y = 12 are (0,0),(0,2),(3,0) and (20/19,45/19)

Corner points	Z = 5x + 3 y
O(0 , 0 )	0
B ( 2 , 0 )	10
C( 0 , 3 )	9
D ( 20/19 , 45/19 )	235/19 ……………….(Max.)

Here , Z = -12 is minimum at C ( 4 , 0 ) .

Relations and Functions Prepare / Learn

Q2. A relation R from C(complex no.) to R(real no.) is defined by x Ry iff |x| = y. Which of the following is correct?

A. (1 + i)R2

B. iR1

C. 3R(–3)

D. (2 + 3 i)R13

Answer : Option B
Explaination / Solution:

As

x \in C

i.e. x is a complex no., then

| i | = \sqrt{0^{2} + 1^{2}} = 1

Determinants Prepare / Learn

Q3. The only integral root of the equation det.

A. 2

B. 4

C. 3

D. 1

Answer : Option D
Explaination / Solution:

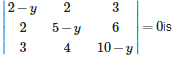
The value of determinant is 0 if any two rows or column are identical and Clearly , y = 1 satisfies it. $[C_{3} = 3 C_{1}]$

if we take common as 3 from C3 THEN C1 And C3 Becomes identical after puting y=1.

Integrals Prepare / Learn

Q4.

\int (\tan x + c o t x)

dx is equal to

A. none of these.

B. log | sin x + cos x|+C

C. log | cot x|+C

D. log | tan x|+C

Answer : Option D
Explaination / Solution:

[−log| cosx|+log| sin x|]=log | tan x|+C

Vector Algebra Prepare / Learn

Q5. If a vector

\vec{r}

is expressed in component form as

\vec{r} = x \hat{i} + y \hat{j} + z \hat{k}

then x, y and z are referred to as

A. unit scalars

B. scaling factors

C. vector components or rectangular components

D. unit vectors

Answer : Option C
Explaination / Solution:

In

\vec{r}

\vec{r} = x \hat{i} + y \hat{j} + z \hat{k}

x , y and z represents the components of

\vec{r}

along x-axis ,y-axis and z-axis respectively.

Probability Prepare / Learn

Q6. Compute P(A|B), if P(B) = 0.5 and P (A ∩ B) = 0.32

A. P(A|B) =

\frac{16}{33}

B. P(A|B) =

\frac{16}{33}

C. P(A|B) =

\frac{15}{27}

D. P(A|B) =

\frac{16}{29}

Answer : Option A
Explaination / Solution:

We have , P(B) = 0.5 and P (A ∩ B) = 0.32

P (A / B) = \frac{P (A \cap B)}{P (B)} = \frac{0.32}{0.5} = \frac{16}{25}

Inverse Trigonometric Functions Prepare / Learn

Q7. The range of

\tan^{- 1}

x is

A. (π,π)

B. R

C. [−π2,π2]

D. [-π2,π2]

Answer : Option D
Explaination / Solution:

the domain range of tan function are $(- \frac{π}{2}, \frac{π}{2})$ and R

But tan function is one one and onto only when we shrink range to (-1,1)

Now tan function which is one and on to has domain $(- \frac{π}{2}, \frac{π}{2})$ and range(-1,1)

hence domain and range of $\tan^{- 1}$ function is (-1,1 ) to $(- \frac{π}{2}, \frac{π}{2})$

Continuity and Differentiability Prepare / Learn

Q8. If x + | y | = 2y , then y as a function of x is

A. not continuous at x = 0

B. not defined for all real x

C. such that dy/dx = 1/3 for x<0

D. differentiable for all x

Answer : Option C
Explaination / Solution:

Three Dimensional Geometry Prepare / Learn

Q9. Find the vector equations of the line that passes through the points (3, – 2, – 5), (3, – 2, 6).

Answer : Option C
Explaination / Solution:

Here ,

\vec{a} = - 3 \hat{i} - 2 \hat{j} - 5 \hat{k}

and

\vec{b} = 0 \hat{i} + 0 \hat{j} + 11 \hat{k}

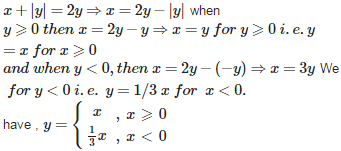
Therefore , the vector equation is :

\vec{r} = \vec{a} + λ \vec{b}

i.e.

\vec{r} = 3 \hat{i} - 2 \hat{j} - 5 \hat{k} + λ (11 \hat{k} .)

Differential Equations Prepare / Learn

Q10. General solution of

(e^{x} + e^{- x}) d y - (e^{x} - e^{- x}) d x = 0

A. y = log(e−2x+ e−x) + C

B. y = log(e2x+ e−x) + C

C. y = log(ex+ e−x) + C

D. y = (ex+ e−x) + C

Answer : Option C
Explaination / Solution:

(e^{x} + e^{- x}) d y = (e^{x} - e^{- x}) d x \int d y = \int \frac{(e^{x} - e^{- x})}{(e^{x} + e^{- x})} d x y = \log | (e^{x} + e^{- x}) | + C

Since

\int \frac{f^{'} (x)}{f (x)} d x = l n f (x) + c

CBSE 12TH MATHEMATICS - Online Test

Prepare Before Start Test | Learn

UPSC Civil services Entrance exams | Online Test

GATE Exam | Online Test

Under Graduate Entrance Exams | Online Test

Problem Solving and Reasoning | Online Test

CAT Entrance Exams | Online Test

CLAT LAW Entrance exams | Online Test

Banking Entrance exams | Online Test

UGC NET Entrance exams | Online Test

TANCET Anna University | Online Test

TN State Board | Online Test