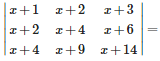cbse 12th mathematics | Online Objective Test

Q1. If E, F and G are events with P(G) ≠ 0 then P ((E ∪ F)|G) given by

A. P (G|E) + P (F|G) – P ((E ∩ F)|E)

B. P (E|G) + P (G|F) – P ((E ∩ F)|G)

C. P (E|G) + P (F|G) – P ((E ∩ F)|G)

D. P (E|G) + P (F|G) – P ((E ∩ F)|F)

Answer : Option C
Explaination / Solution:

P(EUF/G) = $\frac{P [(E U F) \cap G]}{P (G)}$ = $\frac{P [(E \cap G) U (F \cap G]}{P (G)}$ $\frac{P (E \cap G) + P (F \cap G) - P (E \cap G \cap F \cap G) }{P (G)}$

= $\frac{P (E \cap G) }{P (G)}$ + $\frac{P (F \cap G) }{P (G)}$ - $\frac{P (E \cap F \cap G) }{P (G)}$

= P (E|G) + P (F|G) – P ((E ∩ F)|G)

Inverse Trigonometric Functions Prepare / Learn

Q2. If sin A + cos A = 1, then sin 2A is equal to

A. 1/2

B. 1

C. 2

D. 0

Answer : Option D
Explaination / Solution:

$(Sin A + Cos A)^{2} = s i n^{2} A + c o s^{2} A + 2 s i n A c o s A$

1 = 1 + Sin 2A

so, Sin 2A = 0

Hence A = 0

Continuity and Differentiability Prepare / Learn

Q3. If f(x) = x | x | ∀x∈R, then

A. f is derivable at x = 0 but f’ (0) ≠

B. none of these

C. f is discontinuous at x = 0

D. f is derivable at x = 0 and f ‘ (0) = 1

Answer : Option B
Explaination / Solution:

$\begin{array}{l} H e r e, f (x) = x | x, | \\ w h i c h i s p r o d u c t o f t w o c o n t i n u o u s f u n c t i o n s, \\ H e n c e f i s c o n t i n u o u s \forall x \in R \end{array}$

Also, f'(x) $= x . \frac{x}{| x |} + | x | .1$
$= | x + | | x | = 2 | x |$ ,

Therefore f'(x) exists at all $x \in R$

Further, f'(0) = $2. | 0 | = 0$

Differential Equations Prepare / Learn

Q4. The number of arbitrary constants in the general solution of a differential equation of fourth order are:

A. 2

B. 3

C. 4

D. 1

Answer : Option C
Explaination / Solution:

4 , because the no. of arbitrary constants is equal to order of the differential equation.

Three Dimensional Geometry Prepare / Learn

Q5.

If a line makes angles

90^{\circ}, 135^{\circ}, 45^{\circ}

with the x, y and z – axes respectively, find its direction cosines.

A. 0,−12√,15√

B. 1,−13√,12√

C. 0,−12√,13√

D. 0,−12√,12√

Answer : Option D
Explaination / Solution:

If a line makes angles

90^{\circ}, 135^{\circ}, 45^{\circ}

with the x, y and z – axes respectively, then the direction cosines of this line is given by :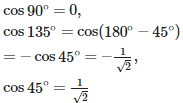

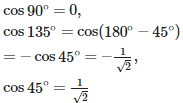
\cos 90^{\circ} = 0, \cos 135^{\circ} = \cos (180^{\circ} - 45^{\circ}) = - \cos 45^{\circ} = - \frac{1}{\sqrt{2}}, \cos 45^{\circ} = \frac{1}{\sqrt{2}}

Matrices Prepare / Learn

Q6.

A square matrix A = ${[a_{i j}]}_{n \times n}$ is called a lower triangular matrix if $a_{i j} = 0$ for

A. i is less than j

B. i = j

C. is greater than j

D. none of these.

Answer : Option A
Explaination / Solution:

Lower triangular matrix is given by : $[\begin{matrix} a_{11} & 0 & 0 \\ a_{21} & a_{22} & 0 \\ a_{31} & a_{32} & a_{33} \end{matrix}]$ Here, $a_{i j} = 0$ , if i is less than j.and $a_{i j} \neq 0$ , if i is greater than j.

Application of Integrals Prepare / Learn

Q7. Area bounded by the curves satisfying the conditions

\frac{x^{2}}{25} + \frac{y^{2}}{36} ⩽ 1 ⩽ \frac{x}{5} + \frac{y}{6}

is given by

A. 15(π/2 - 1 ) sq. units

B. 15/4 (π/2 - 1 ) sq. units

C. 15/2 (π/2 - 1 ) sq. units

D. 30 ( - 1 ) sq. units

Answer : Option A
Explaination / Solution:

Linear Programming Prepare / Learn

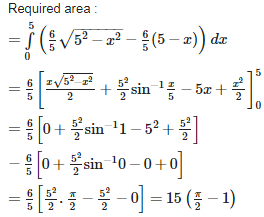
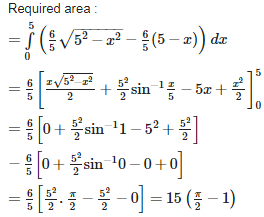
Q8. In a LPP if the objective function Z = ax + by has the same maximum value on two corner points of the feasible region, then every point on the line segment joining these two points give the same

A. Minimum value

B. Mean value

C. Maximum value

D. Upper limit value

Answer : Option C
Explaination / Solution:

In a LPP if the objective function Z = ax + by has the same maximum value on two corner points of the feasible region, then every point on the line segment joining these two points give the same maximum value . If the problem has multiple optimal soliutions at the corner points, then both the points will have the same (maximum or minimum)value.

Relations and Functions Prepare / Learn

Q9. The void relation ( a subset of A x A ) on a non empty set A is :

A. only transitive

B. Reflexive

C. Transitive and symmetric

D. only symmetric

Answer : Option C
Explaination / Solution:

The relation { }⊂ A x A on a is surely not reflexive.However ,neither symmetry nor transitivity is contradicted .So { } is a transitive and symmetric relation on A.

CBSE 12TH MATHEMATICS - Online Test

Prepare Before Start Test | Learn

UPSC Civil services Entrance exams | Online Test

GATE Exam | Online Test

Under Graduate Entrance Exams | Online Test

Problem Solving and Reasoning | Online Test

CAT Entrance Exams | Online Test

CLAT LAW Entrance exams | Online Test

Banking Entrance exams | Online Test

UGC NET Entrance exams | Online Test

TANCET Anna University | Online Test

TN State Board | Online Test