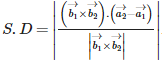CBSE 12TH MATHEMATICS - Online Test
Conditions for the partition sub-sets to be an equivalence relation:
(i) The partition sub-sets must be disjoint i.e.their is no common elements between them
(ii) Their union must be equal to the main set (super-set)
Here the set A={1,2,3,4,5,6},the partition sub-sets {1,3},{2,4,5},{6} are pairwise disjoint and their union i.e. {1,3} U {2,4,5} U {6} = {1,2,3,4,5,6} = A,which is the condition for the partition sub-sets to be an equivalence relation of the set A.
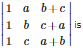

since C1 And C2 are identical
=(a+b+c)x0 =0
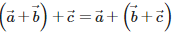
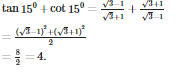
Case 1 Let c be a real number which is not equal to any integer. for all real numbers close to c the value of the function is equal to [c]; i.e., . Also and hence the function is continuous at all real numbers not equal to integers.
Case 2 Let c be an integer. Then we can find a sufficiently small real number such that
This, in terms of limits mean that
Since these limits cannot be equal to each other for any c, the function is discontinuous at every integral point.
is given by :