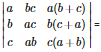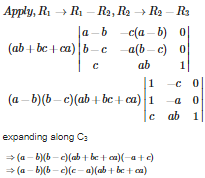CBSE 12TH MATHEMATICS - Online Test
Q1.
Let ( be a partition of a sample space and suppose that each of has nonzero probability. Let A be any event associated with S,then
Answer : Option A
Explaination / Solution:
Let {E1, E2, ...,En) be a partition of a sample space and suppose that each of E1, E2, ..., En has nonzero probability. Let A be any event associated with S,then P(A) = P(E1) P (A|E1) + P (E2) P (A|E2) + ... + P (En) P(A|En) .by addition law of probability.
Q2. If is equal to
Answer : Option A
Explaination / Solution:
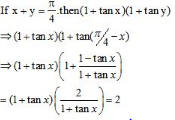
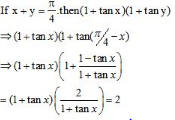
Q3.
is equal to
Answer : Option B
Explaination / Solution:
limx→0tanxlog(1+x)=limx→0tanxxxlog(1+x)=limx→0tanxx.limx→011xlog(1+x)=1.11=1
Q4. Determine order and degree (if defined) of
Answer : Option B
Explaination / Solution:
Order = 2 , degree = 1 .Since the highest derivative term is and its power is 1
Q5. Vector equation of a line that passes through two points whose position vectors are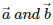 
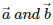is
is
Answer : Option D
Explaination / Solution:
Vector equation of a line that passes through two points whose position vectors are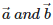 
is given by: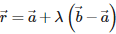 
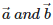is given by: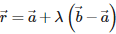
Q6. The area bounded by the curve and the x –axis is
Answer : Option B
Explaination / Solution:
The given curve consists of two straight lines x + y = 1 ( x ≥ 0 )and -x + y = 1 ( x < 0 )
Required area :
= = == = 1sq.unit
Required area :
= = == = 1sq.unit
Q7. If is a square root of the identity matrix, then a, b, c satisfy the relation
Answer : Option B
Explaination / Solution:
⎡⎣⎢⎢⎢acb−a⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢acb−a⎤⎦⎥⎥⎥=⎡⎣⎢⎢⎢1001⎤⎦⎥⎥⎥⇒a2+bc=1
Q8.
At (0, 0) the curve
Answer : Option D
Explaination / Solution:
and hence the tangent to the curve at ( 0 , 0 ) makes an angle of with +ve X-axis.
Q10. In Corner point method for solving a linear programming problem one finds the feasible region of the linear programming problem ,determines its corner points and evaluates the objective function Z = ax + by at each corner point. If M and m respectively be the largest and smallest values at corner points then
Answer : Option B
Explaination / Solution:
In Corner point method for solving a linear programming problem one finds the feasible region of the linear programming problem ,determines its corner points and evaluates the objective function Z = ax + by at each corner point. If Mand m respectively be the largest and smallest values at corner points then If the feasible region is bounded, M and m respectively are the maximum and minimum values of the objective function .
