CBSE 11TH MATHEMATICS - Online Test

Answer : Option B
Explaination / Solution:

Answer : Option B
Explaination / Solution:

Answer : Option C
Explaination / Solution:

Answer : Option B
Explaination / Solution:

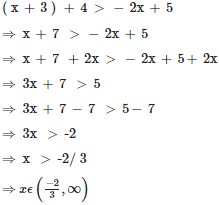
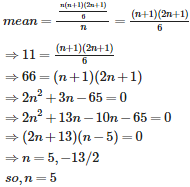
The equation 4x + 5y = 20 can be written as x5+y4 = 1

This implies the intercepts cut by this line on the X and Y axes  are 5 and 4 respectively.

Hence the area of the triangle is 1/2 [ 5 x 4] = 10 square units

Answer : Option B
Explaination / Solution:

(∼p∨∼q∨p∨q)   Since p∨(q∨r)≡(p∨q)∨r

∼p∨p≡T

Hence tautology

Answer : Option A
Explaination / Solution:

The given equation of the circle can be written as 

(x-1)2 - 1 + (y- 2)2 - 4 = 0

(x - 1)2 + (y + 2)2 = 5

This implies the radius is 5–√ and the centre is (1,-2)

The given point is (-1,2)

The distance between the centre of the  circle and the given point is

(−1−1)2+(2+2)2−−−−−−−−−−−−−−−−√ = 2–√0

Sice this is greater than the radius, the point lies outside the circle. Hence two tangents can be drawn.

Answer : Option D
Explaination / Solution:

This criteria is from the basic principle of mathematical induction.

Answer : Option D
Explaination / Solution:

cosecA(sinBcosC+cosBsinC)=cosecA.sin(B+C)[∵A+B+C=π]=sin(B+C)sinA=sin(π−A)sinA=sinAsinA=1

Answer : Option B
Explaination / Solution:

The number of selections of r objects from the given n objects is denoted by nCr and we have nCr=n!r!(n−r)! 

Now n ties can be selected from a rack displaying 3n different ties in   3nCn=3n!n!(3n−n)!=3n!n!(2n)!   different ways

Answer : Option A
Explaination / Solution:
No Explaination.