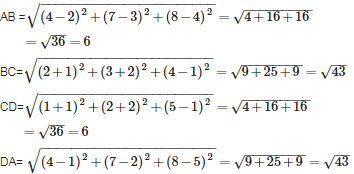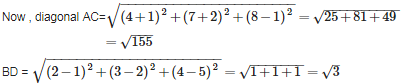Introduction to Three Dimensional Geometry - Online Test
The distance of the point ( 3, 4, 5) from X- axis is
let L be the foot of perpendicular from the point ( 3, 4, 5) to X axis ,then coordinate of L will be (3,0,0) [ because on X axis y and z coordinate are zero]
then distance of the point ( 3, 4, 5) from X- axis i.e. from L (3,0,0) is given by =
As we know that if a lines makes angles a , b and c with X-axis , Y-axis and Z-axis respectively then direction cosines are given by < cos a , cos b ,cos c >
In our case line is X-axis itself which we know makes angle of 0 , 90 , 90 with X-axis , Y-axis and Z-axis respectively then direction cosine will be
<cos 0 , cos 90, cos 90>
= < 1 0 0 >
Concept used - Parellel lines have same direction cosines
Explanation We know Z axis is perpendicular to XY plane and direction cosines of Z axis are <0,0,1>
and as any normal to XY plane will be parallel to Z axis and parellel lines have same direction cosines so answer is <0,0,1>
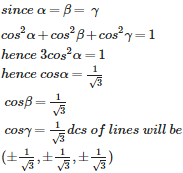
We know that if l , m , n are direction cosines of a lines then l2+m2 +n2= 1
so, k2 + k2 +k2 = 1
3 k2 = 1
k2 = 1/3
taking squareroot on both sides , we have
we know that general equation of sphere is
since sphere passing through the points ( 4 ,3 , 0 ) , ( 0 , 4 , 3 ) ,( 0 , 5 , 0 ) and ( 4 , 0 , 3 ) so putting these values one by one in given equation , we get
16+ 9+ 8g + 6f + c=0 =>8g +6f +c = -25 -------------1)
16 +9 +8f +6h +c=0 =>8f + 6h +c= -25 -----------2)
25 + 10f +c = 0 -----------------------3)
16+ 9+ 8g + 6h +c=0 =>8g +6h +c= -25 -------------4)
by 2) - 4 ) we have f = g
using this in 1) we have 16f +c = -25 -------5)
Now solving 3) and 5) we get f=0
using value of f we have g= 0 , h= 0 , c= -25
Now radius = = =5