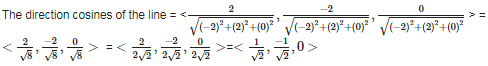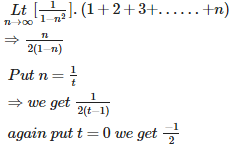CBSE 11TH MATHEMATICS - Online Test
Q2. Sum of all 2 digit odd numbers is
Answer : Option D
Explaination / Solution:
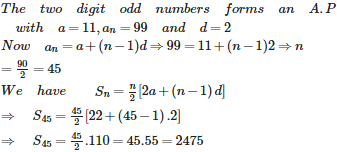
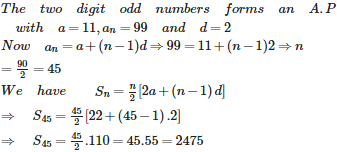
Q3. If the coefficient of variation between x and y is 0.28, covariance between x and y is 7.6, and the variance of x is 9, then the S.D. of the y series is
Answer : Option C
Explaination / Solution:
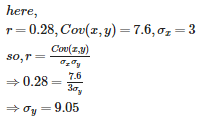
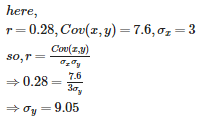
Q4. The lines x + ( k – 1) y + 1 = 0 and are at right angles if
Answer : Option A
Explaination / Solution:
If the lines are at right angles to each other, then the product of their slopes = -1. Slope of any line = -(coefficient of x/coeffiecient of y)
Therefore slope of line 1 = -(1/(k-1)
Slope of line 2 = -2/k2
Therefore X = - 1
That is k2 (k-1) = -2
i.e; k3 - k2 +2 = 0
On factorizing we get (k+1)(k2 -2k - 2) = 0
This imlpies k+1 is a factor, hence k = -1
Hence they are at right angles if k = -1
Q5. The compound statement p→(∼p∨q) is false , then the truth values of p and q are respectively
Answer : Option B
Explaination / Solution:
since T->F is false.
Hence q=F.
So p=T and q=F
Q6. The equation represents
Answer : Option B
Explaination / Solution:
On factorizing the given equation we get y+x-1=0 and y-x+1=0, which clearly represent a pair of straight lines which are intersecting.
Q7. The statement P ( n ) : “ “ is true for :
Answer : Option D
Explaination / Solution:
When n = 1 we get 16>16, which is false. when n = 2 we get 25>32,which is false as well. As n = 3,4,5....the inequalty does not hold correct.
Q8.
If then is equal to
Answer : Option C
Explaination / Solution:
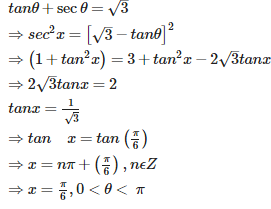
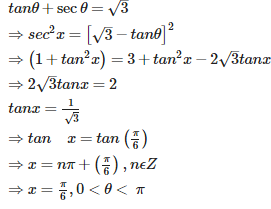
Q9. A coin is tossed n times, the number of all the possible outcomes is
Answer : Option D
Explaination / Solution:
There can either be a heads or tails, therefore for every toss, the possible outcomes are 2. hence for n number of toss the possibilities are 2n.
Q10. The direction cosines of the line joining ( 1 , - 1 , 1 ) , and ( -1 , 1 , 1 ) are
Answer : Option C
Explaination / Solution:
The direction ratio of the line joining ( x1 , y1 , z1 ) , and ( x2 , y2 , z2) = < x1-x2 , y1-y2 , z1-z2 >
The direction ratio of the line joining ( 1 , - 1 , 1 ) , and ( -1 , 1 , 1 ) = < 1+1 , -1-1 , 1-1> = < 2 , -2 , 0 >