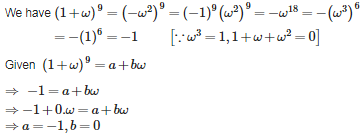CBSE 11TH MATHEMATICS - Online Test

Answer : Option A
Explaination / Solution:

sum of weights of 10 items =280

sum of weights of n items = 35n

so, sum of weights of ( 10 + n) items = 280 + 35n

so ,mean = (280 + 35 n) / ( 10 + n)

30(10 + n ) = 280 + 35n 

solving we get, n = 4

 

Answer : Option B
Explaination / Solution:

The perpendicular distance from the origin to the line is given by Ax1+By1+CA2+B2√

For the given line c = 1, A = 3 and B = 4 and since it passes through the origin,

Sustituting the values we get,

19+16√ = 1/5

Answer : Option B
Explaination / Solution:

∼(p∧q)≡∼p∨∼q De Morgan's law

Answer : Option C
Explaination / Solution:

When n = 1 we have 391 which is divisible by 17.

Answer : Option B
Explaination / Solution:

The angle between the Radius and tangent is 900

Answer : Option C
Explaination / Solution:

Answer : Option C
Explaination / Solution:

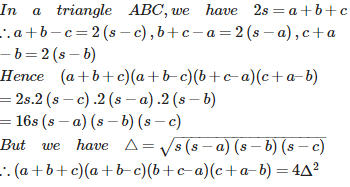
Case 1: for 5 digit numbers Ten Tens thousands place can be occupied in 4 ways since 0 cannot be suitable. For ones place remaining 4 numbers ( since repetition is not allowed ) can be occupied in 4 ways : and the tens place in 3 ways and hundreds place in 2 ways and the thousands place in 1 way. Hence the total number of ways is 4x1x4x2x3= 96.

t th	th	h	t	o
4	1	2	3	4

Case 2: for 4 digit numbers thousands place can be occupied in 4 ways since 0 cannot be suitable. For ones place remaining 4 numbers ( since repetition is not allowed ) can be occupied in 4 ways : and the tens place in 3 ways and hundreds place in 2 ways . Hence the total number of ways is 4x4x2x3= 96.

th	h	t	o
4	2	3	4

Case 3: for 3digit numbers hundreds place can be occupied in 4 ways since 0 cannot be suitable. For ones place remaining 4 numbers ( since repetition is not allowed ) can be occupied in 4 ways : and the tens place in 3 ways  Hence the total number of ways is 4x4x3= 48

Case 4: for 2 digit numbers Tens place can be occupied in 4 ways since 0 cannot be suitable. For ones place remaining 4 numbers ( since repetition is not allowed ) can be occupied. Hence the total number of ways is 4x4=16.

Case 5: For single digit in 4 ways .

Hence 96 + 96 + 48+ 16+4 = 260

Answer : Option C
Explaination / Solution:

A point ( x , y , z ) moves parallel to X- axis then value of x will vary and remaining will be fixed

Answer : Option B
Explaination / Solution:

Answer : Option A
Explaination / Solution: