CBSE 11TH MATHEMATICS - Online Test
Q1. Let p and q be two propositions. Then, the contrapositive of the implication p→q is
Answer : Option B
Explaination / Solution:
the contrapositve of p→q is∼q→∼p
Q2. The inequality is true for :
Answer : Option B
Explaination / Solution:
When n = 1 we get , and when n = 2 we get ,. when n = 3 , which are inavlid inequations. Only when n = 4 we get , which is valid.
Q3. The number of points on X-axis which are at a distance c units (c 3) from ( 2, 3) is
Answer : Option B
Explaination / Solution:
the shortest distance from x-axis to the point is 3.
Q4.
In a triangle ABC, a = 2b and then angle A is
Answer : Option D
Explaination / Solution:
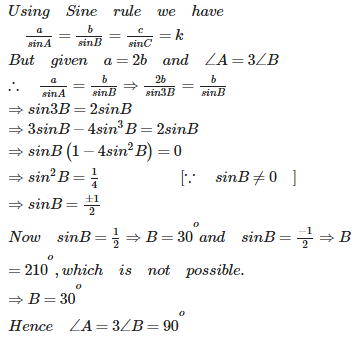
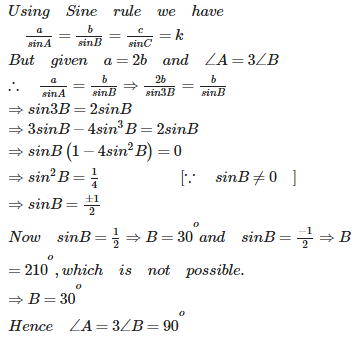
Q5. The number of different ways in which a man can invite one or more of his 6 friends to dinner is?
Answer : Option B
Explaination / Solution:
He can invite any one friend in 6C1 ways= 6 ways:
He can invite any two friends in 6C2 ways = 15 ways
He can invite any three friends in 6C3 ways =20 ways
He can invite any 4 friends in 6C4ways = 15 ways
He can invite any 5 friends in 6C5 ways = 6 ways
He can invite all the 6 friends in 6C6 ways= 1 way.
Since any one of these could happen total possibilities are, 6+15+20+15+6+1 = 63.
Q6. The lines having drs as a1a2+b1b2+c1c2=0 are
Answer : Option C
Explaination / Solution:
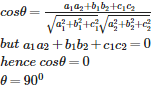
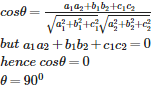
Hence lines are perpendicular
Q7. up to 2k + 1 terms , for all k belongs to natural numbers N .
Answer : Option B
Explaination / Solution:
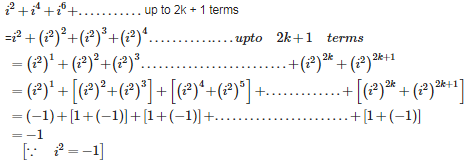
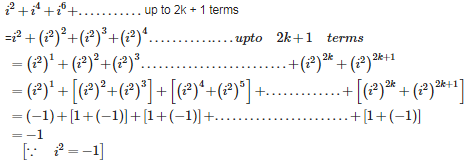
Q8. If A and B are two sets , then A∩(A∪B) is equal to
Answer : Option A
Explaination / Solution:
LetA={1,2,3,4}andB={1,2,3,4,5,6}HereA∪B={1,2,3,4,5,6}NowA∩(A∪B)={1,2,3,4,}=A
Q9. The term independent of x in the expansion of is
Answer : Option B
Explaination / Solution:


Q10. The longest side of a triangle is three times the shortest side and the third side is 2cm shorter than the longest side if the perimeter of the triangles at least 61cm, find the minimum length of the shortest side.
Answer : Option D
Explaination / Solution:
Let the shortest side of a triangle be x cm.Then the length of the longest side is3x cm and the length of the third side is (3x-2) cm.
Given the perimeter of the triangles at least 61cm
Hence the minimum length of the shortest side = 9 cm
