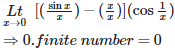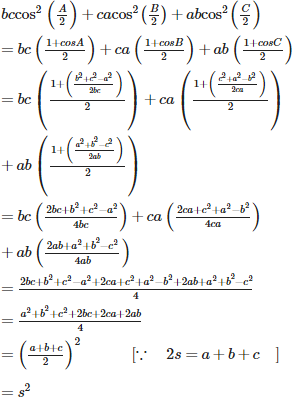CBSE 11TH MATHEMATICS - Online Test

Answer : Option D
Explaination / Solution:

Answer : Option D
Explaination / Solution:

Answer : Option D
Explaination / Solution:

As A/M is calculated as the sum of all the observations divided by number of observations, so it is affected by if there is any change in the outliers

Answer : Option B
Explaination / Solution:

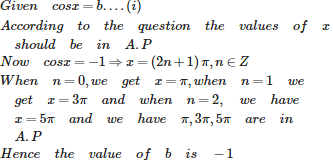
Let the equation of the line which has equal intercepts be 

xa + ya =1

Substituting the values for x and y

1 -2 =a

Therefore a = -1

Hence the equation of the line is x+y+1=0

Answer : Option C
Explaination / Solution:

p↔q≡(p→q)∧(q→p)

Answer : Option A
Explaination / Solution:

when n = 1 the value is 64. By induction process the consecutive replacement of n = 2,3,4....will be multiples of 64.

Answer : Option D
Explaination / Solution:

recalling the general form of a circle as

(i) It is a quadratic equation in both x and y.

(ii) Coefficient of x2  = Coefficient of y2   .

(iii) There is no term containing xy i.e., the coefficient of xy is zero.

(iv) radius is 1ag2+f2−ca−−−−−−−−−√ 

To satisfy (i) and (ii) condition we have a=b≠0 

To satisfy (iii) condition we have h=0

To satisfy (iv) and as we cant have neagtive sign in root so g2+f2−ac>0

Answer : Option A
Explaination / Solution:

First we will fix any one digit in a fixed position .Then we have the remaining 4 digits can be arranged in 4! different ways.

Which means each of the five digits can appear in each of the five places in  4! times.

Hence the sum of the digits in each position is 4!(1+3+5+7+9)=25×4!

Now to find the sum  of these numbers formed we have to consider the place values  for these digits

So the sum of all the numbers which can be formed by using the digits 1 , 3 , 5 , 7 ,9=25×4!×(1+10+100+1000+10000)=25×4!×11111=666660

 

Answer : Option D
Explaination / Solution:

Answer : Option B
Explaination / Solution:
No Explaination.