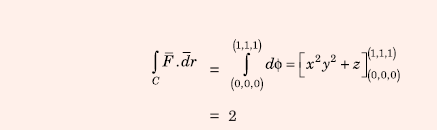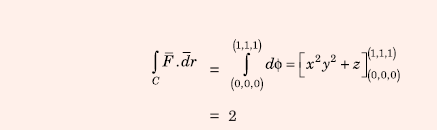Electromagnetic Fields - Online Test
Q1. Given a vector field 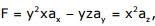 the line integral ∫ F.dl evaluated along
a segment on the x-axis from x=1 to x=2 is
the line integral ∫ F.dl evaluated along
a segment on the x-axis from x=1 to x=2 is
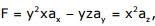 the line integral ∫ F.dl evaluated along
a segment on the x-axis from x=1 to x=2 is
the line integral ∫ F.dl evaluated along
a segment on the x-axis from x=1 to x=2 is
Answer : Option B
Explaination / Solution:
No Explaination.
Q2. The curl of the gradient of the scalar field defined by V = 2x2y + 3y2z + 4z2x is
Answer : Option D
Explaination / Solution:
No Explaination.
Q3. The flux density at a point in space is given by  The value of constant k must be equal to
The value of constant k must be equal to
 The value of constant k must be equal to
The value of constant k must be equal to
Answer : Option A
Explaination / Solution:
No Explaination.
Q4. A dielectric slab with 500mm x 500mm cross-section is 0.4m long. The slab is
subjected to a uniform electric field of 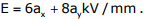 . The relative
permittivity of the dielectric material is equal to 2. The value of constant ε0 is 8.85 × 10-12 F/m. The energy stored in the dielectric in Joules is
. The relative
permittivity of the dielectric material is equal to 2. The value of constant ε0 is 8.85 × 10-12 F/m. The energy stored in the dielectric in Joules is
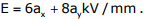 . The relative
permittivity of the dielectric material is equal to 2. The value of constant ε0 is 8.85 × 10-12 F/m. The energy stored in the dielectric in Joules is
. The relative
permittivity of the dielectric material is equal to 2. The value of constant ε0 is 8.85 × 10-12 F/m. The energy stored in the dielectric in Joules is
Answer : Option B
Explaination / Solution:
No Explaination.
Q5. The magnitude of magnetic flux density 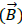 at a point having normal distance d meters from
an infinitely extended wire carrying current of l A is
at a point having normal distance d meters from
an infinitely extended wire carrying current of l A is 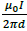 (in SI units). An infinitely
extended wire is laid along the x-axis and is carrying current of 4 A in the +ve x direction.
Another infinitely extended wire is laid along the y-axis and is carrying 2 A current in the +ve
y direction µ0 is permeability of free space Assume
(in SI units). An infinitely
extended wire is laid along the x-axis and is carrying current of 4 A in the +ve x direction.
Another infinitely extended wire is laid along the y-axis and is carrying 2 A current in the +ve
y direction µ0 is permeability of free space Assume 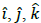 to be unit vectors along x, y and
z axes respectively.
to be unit vectors along x, y and
z axes respectively.
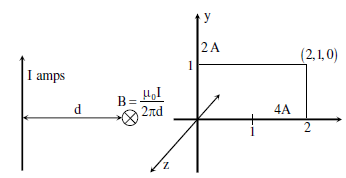

Assuming right handed coordinate system, magnetic field intensity, 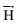 at coordinate (2,1,0)
will be
at coordinate (2,1,0)
will be
Answer : Option C
Explaination / Solution:
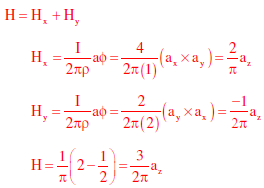
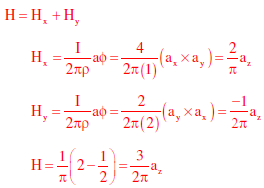
Q6. Match the following

Answer : Option B
Explaination / Solution:
No Explaination.
Q7. Two semi-infinite dielectric regions are separated by a plane boundary at y=0. The
dielectric constant of region 1 (y<0) and region 2 (y>0) are 2 and 5, Region 1 has uniform
electric field 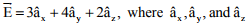 are unit vectors along the x, y and
z axes, respectively. The electric field region 2 is
are unit vectors along the x, y and
z axes, respectively. The electric field region 2 is
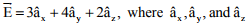 are unit vectors along the x, y and
z axes, respectively. The electric field region 2 is
are unit vectors along the x, y and
z axes, respectively. The electric field region 2 is
Answer : Option A
Explaination / Solution:
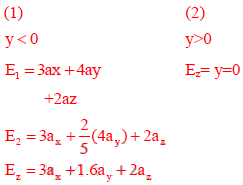
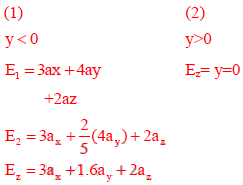
Q8. In cylindrical coordinate system, the potential produced by a uniform ring charge is given by φ = f(r, z), where f is a continuous function of r and z. Let  be the resulting electric field. Then the magnitude of ∇ ×
be the resulting electric field. Then the magnitude of ∇ × 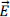
Answer : Option B
Explaination / Solution:


Q9. Two electric charges q and −2q are placed at (0,0) and (6,0) on the x-y plane. The equation of the zero equipotential curve in the x-y plane is
Answer : Option D
Explaination / Solution:
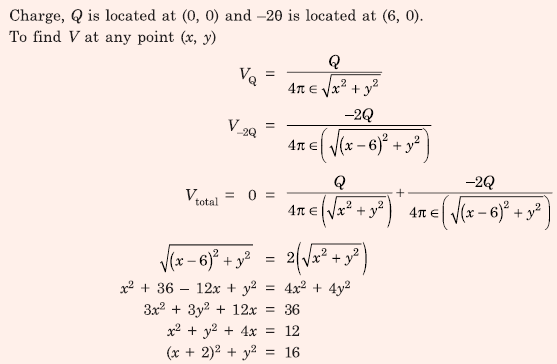
Q10. The value of the line integral
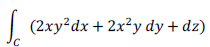
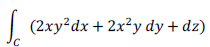
along a path joining the origin (0, 0, 0) and the point (1, 1, 1) is
Answer : Option B
Explaination / Solution: