UNIT VI: Ray Optics - Online Test
Q1. The speed of light in an isotropic medium depends on,
Answer : Option B
Explaination / Solution:
c =
vλ, v is
independent of medium
Q2. A rod of length 10 cm lies along the principal axis of a concave mirror of focal length 10 cm in such a way that its end closer to the pole is 20 cm away from the mirror. The length of the image is,
Answer : Option B
Explaination / Solution:
End
A of the rod acts as an object for mirror and A' will be its image. By mirror
formula, image distance of A is VA.
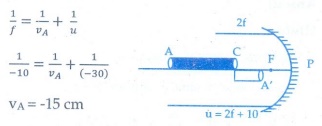
VA
= -15cm
Also
image distance of C
Vc= -20 cm
∴ The length of image = | VA-VC
|
= | -15-(20) | = 5cm
Q3. An object is placed in front of a convex mirror
of focal length of f and the maximum
and minimum distance of an object from the mirror such that the image formed is
real and magnified.
Answer : Option D
Explaination / Solution:
Since the nature of image produced by a convex mirror is always virtual, erect and diminished.
Q4. For light incident from air on a slab of refractive index 2, the maximum possible angle of refraction is,
Answer : Option A
Explaination / Solution:
n= 2;
i=90◦
n = sin i / sin r
sin
r = sin i / n
= sin 90◦/2 = ½
r
= sin-1(1/2) = 30◦
Q5. If the velocity and wavelength of light in air
is Va and λa and that in water is Vw and λ ,
then the refractive index of water is,
Answer : Option B
Explaination / Solution:
n = speed of light in vacuum / speed of light in
medium =Va / Vw
Q6. Stars twinkle due to,
Answer : Option C
Explaination / Solution:
No Explaination.
Q7. When a biconvex lens of glass having refractive index 1.47 is dipped in a liquid, it acts as a plane sheet of glass. This implies that the liquid must have refractive index,
Answer : Option D
Explaination / Solution:
Since the liquid act as a plane sheet of glass its refractive index is equal to that of glass.
Q8. The radius of curvature of curved surface at a thin planoconvex lens is 10 cm and the refractive index is 1.5. If the plane surface is silvered, then the focal length will be,
Answer : Option B
Explaination / Solution:
For
a plano-convex lens with its plane surface silvered
1/f = 2(n − 1)/R
f = R / 2(n − 1) = 10 / 2(1.5 − 1) = 10 / 2(0.5) = 10 cm
Q9. An air bubble in glass slab of refractive index 1.5 (near normal incidence) is 5 cm deep when viewed from one surface and 3 cm deep when viewed from the opposite face. The thickness of the slab is,
Answer : Option C
Explaination / Solution:
n
- 1.5 ; d' = nd
In
one side bubble depth is 5 cm
∴ Original depth = 1.5 x 5 = 7.5 cm
On
the other side depth is 3 cm
∴ Original depth = 1.5 x 3 = 4.5
cm
∴ Thickness is 7.5 + 4.5 = 12 cm
Q10. A ray of light travelling
in a transparent medium of refractive index n falls, on a surface separating
the medium from air at an angle of incidents of 45º. The ray can undergo total
internal reflection for the following n,
Answer : Option D
Explaination / Solution:
For
total internal reflection
i > C;
sin
i > sin C;
sin
45◦ > 1/n
1/√2
> 1/n
n>√2
n>1.414
Here, n=1.5
