Probability - Online Test
Q1. If A and B are two events such that A ⊂ B and P(B) ≠ 0, then which of the following is correct?
Answer : Option A
Explaination / Solution:
since A⊂B A⋂B=AP(A/B)=P(A⋂B)P(B)=P(A)P(B)
Q2. The probability of obtaining an even prime number on each die , when a pair of dice is rolled, is given by :
Answer : Option A
Explaination / Solution:
Clearly , n(s) =36. Favourable cases are { 2, 2 } Therefore required probability = 1/36 .
Q3. A bag contains 4 red and 4 black balls, another bag contains 2 red and 6 black balls. One of the two bags is selected at random and a ball is drawn from the bag which is found to be red. Find the probability that the ball is drawn from the first bag.
Answer : Option A
Explaination / Solution:


Q4.
Answer : Option D
Explaination / Solution:
Let are events of selection of a hostlier and a day scholar respectively.
Let A = event of getting grade A.
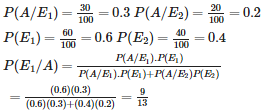
Let A = event of getting grade A.
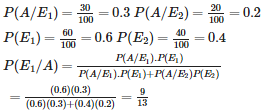
Q5. In answering a question on a multiple choice test, a student either knows the answer or guesses. Let be the probability that he knows the answer and be the probability that he guesses. Assuming that a student who guesses at the answer will be correct with probability . What is the probability that the student knows the answer given that he answered it correctly?
Answer : Option B
Explaination / Solution:
Let are events that the student knows the answer and the student guesses respectively.


Q6. A laboratory blood test is 99% effective in detecting a certain disease when it is in fact, present. However, the test also yields a false positive result for 0.5% of the healthy person tested (i.e. if a healthy person is tested, then, with probability 0.005, the test will imply he has the disease). If 0.1 percent of the population actually has the disease, what is the probability that a person has the disease given that his test result is positive?
Answer : Option A
Explaination / Solution:
Let
are events that a person has disease and the person has not disease. .
Let A = event that the test result is positive.

are events that a person has disease and the person has not disease. .
Let A = event that the test result is positive.

Q7. A random variable is a real valued function whose domain is the.
Answer : Option B
Explaination / Solution:
A random variable is a real valued function whose domain is the sample space of a random experiment .
Q8. Let X be a random variable assuming values x1, x2,....,xn with probabilities p1, p2, ...,pn, respectively such that pi ≥ 0,. Mean of X denoted by is defined as
Answer : Option B
Explaination / Solution:
Let X be a random variable assuming values x1, x2,....,xn with probabilities p1, p2, ...,pn, respectively such that pi ≥ 0,. Mean of X denoted by is defined as: .
Q9. An urn contains 5 red and 2 black balls. Two balls are randomly drawn. Let X represent the number of black balls. What are the possible values of X? Is X a random variable ?
Answer : Option C
Explaination / Solution:
An urn contains 5 red and 2 black balls. Two balls are randomly drawn. Let X represent the number of black balls.therefore the possible values of X = 0 , 1 ,2 . Yes , X is a random variable.
Q10. Let X represent the difference between the number of heads and the number of tails obtained when a coin is tossed 6 times. What are possible values of X?
Answer : Option A
Explaination / Solution:
Let X represent the difference between the number of heads and the number of tails obtained when a coin is tossed 6 times. When a coin is tossed 6 times , we have 64 outcomes which consists of : (i) 6 heads and 0 tails (ii) 5 heads and 1 tail (iii) 4 heads and 2 tails (iv) 3 heads and 3 tails (v) 2 heads and 4 tails (vi) 1 head and 5 tails (vii) 0 head and 6 tails . Let X represents the difference between the number of heads and tails. (i) X = 6 – 0 = 6 (ii) X = 5 – 1 = 4 (iii) X = 4 – 2 = 2 (iv) X = 3 – 3 = 0 (v) X = 4 – 2 = 2 (vi) X = 5 – 1 = 4 (vii) X = 6 – 0 = 6 . Therefore , X = 6 , 4 , 2, 0 .
