Limits and Derivatives - Online Test
Q1. is equal to
Answer : Option B
Explaination / Solution:
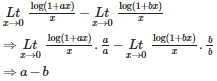
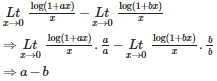
Q2. is equal to
Answer : Option D
Explaination / Solution:
Since when we put x=0, we get 0/0 form, So we have to use D'L hospital rule :
Do the differentiation of numerator and denominator partially w.r.t x , we get :
By putting x=0 directly, we get 0.
Q3. Let f (x) = x sin, x0, then the value of the function at x = 0, so that f is continuous at x = 0, is
Answer : Option D
Explaination / Solution:
Here, if we directly put x= 0, f(0) = 0 * sin (1/0) = 0.
At L.H.L, put x=0-h ,f(0-h) = = 0.
At R.H.L, put x = 0+h , , f(0+h) = = 0.
Hence, L.H.L = f(0) = R.H.L.
f(x) is continuous at x=0.
Q4. is equal to
Answer : Option C
Explaination / Solution:


Q5. is equal to
Answer : Option C
Explaination / Solution:
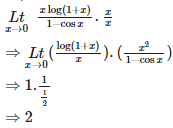
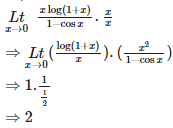
Q6. is equal to
Answer : Option A
Explaination / Solution:
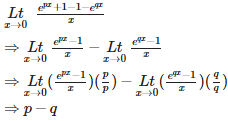
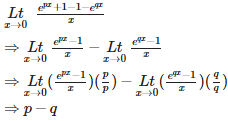
Q7. is
Answer : Option C
Explaination / Solution:
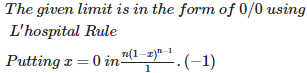
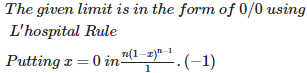
Q8. is equal to
Answer : Option B
Explaination / Solution:


Q9. Ltx→0[cosx]
Answer : Option B
Explaination / Solution:
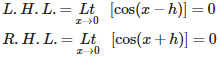
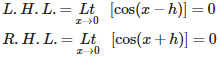
Q10. is equal to
Answer : Option D
Explaination / Solution:
Since the limit is in the form of 0/0. By applying L'hospital first time we get,
Again using L'Hospital;
Again using L'Hospital we get
