Engineering Mathematics - Online Test
Q1. The following surface integral is to be evaluated over a sphere for the given
steady velocity vector field, F = xi + yj + zk defined with respect to a Cartesian
coordinate system having i, j, and k as unit base vectors.
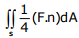
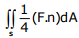
Where S is the sphere, x2 + y2 + z2 = 1 and n is the outward unit normal vector to
the sphere. The value of the surface integral is
Answer : Option A
Explaination / Solution:


Q2. The function f(t) satisfies the differential equation 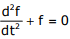 and the auxiliary
conditions,
and the auxiliary
conditions,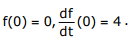 The Laplace transform of f(t) is given by
The Laplace transform of f(t) is given by
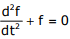 and the auxiliary
conditions,
and the auxiliary
conditions,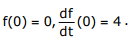 The Laplace transform of f(t) is given by
The Laplace transform of f(t) is given by
Answer : Option C
Explaination / Solution:
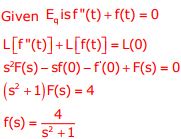
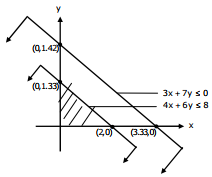
Q3. A linear programming problem is shown below:
Maximize 3x + 7y
3x + 7y ≤ 10
Subject to 4x + 6y ≤ 8
x, y ≥ 0
It has
Answer : Option B
Explaination / Solution:

Q4. The probability that a student knows the correct answer to a multiple choice
question is 2/3. If the student does not know the answer, then the student
guesses the answer. The probability of the guessed answer being correct is 1/4. Given that the student has answered the question correctly, the conditional
probability that the student known the correct answer is
Answer : Option D
Explaination / Solution:
A = The student answer the question correctly 
E1 = Student knows the correct answer
E2 = Student guesses the correct answer

Q5. The solution to the differential equation 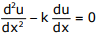 where k is a constant,
subjected to the boundary conditions u(0)=0 and u(L)=U, is
where k is a constant,
subjected to the boundary conditions u(0)=0 and u(L)=U, is
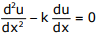 where k is a constant,
subjected to the boundary conditions u(0)=0 and u(L)=U, is
where k is a constant,
subjected to the boundary conditions u(0)=0 and u(L)=U, is
Answer : Option B
Explaination / Solution:
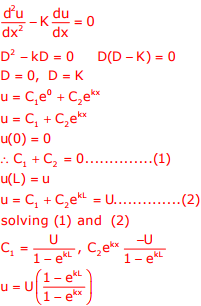
Q6. The value of the definite integral 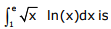
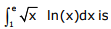
Answer : Option C
Explaination / Solution:
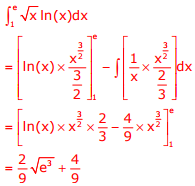
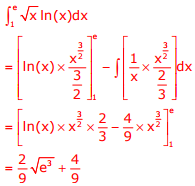
Q7. Find the sum of the expression
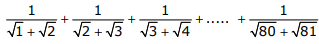
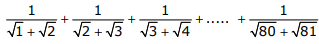
Answer : Option B
Explaination / Solution:
The expression can be written as
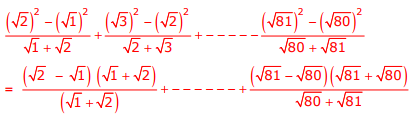
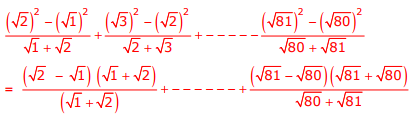
Q8. For a matrix 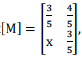 the transpose of the matrix is equal to the inverse of the matrix [M]T = [M]-1. The value of x is given by
the transpose of the matrix is equal to the inverse of the matrix [M]T = [M]-1. The value of x is given by
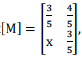 the transpose of the matrix is equal to the inverse of the matrix [M]T = [M]-1. The value of x is given by
the transpose of the matrix is equal to the inverse of the matrix [M]T = [M]-1. The value of x is given by
Answer : Option A
Explaination / Solution:
No Explaination.
Q9. The divergence of the vector field  at a point (1,1,1) is equal to
at a point (1,1,1) is equal to
 at a point (1,1,1) is equal to
at a point (1,1,1) is equal to
Answer : Option C
Explaination / Solution:
No Explaination.
Q10. The inverse Laplace transform of 1/(s2 + s) is
Answer : Option C
Explaination / Solution:
No Explaination.
