Engineering Mathematics - Online Test
Q1. Find the sum of the expression
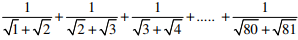
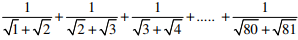
Answer : Option B
Explaination / Solution:
The expression can be written as
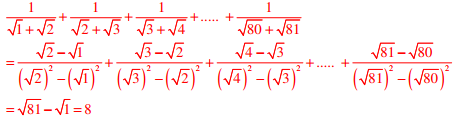
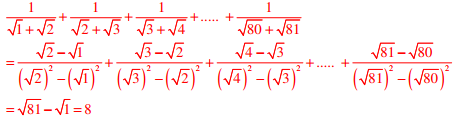
Q2. The current erection cost of a structure is Rs. 13,200. If the labour wages per day increase by
1/5 of the current wages and the working hours decrease by 1/24 of the current period, then
the new cost of erection in Rs. is
Answer : Option B
Explaination / Solution:
Let ‘W’ be the labour wages, and ‘T’ be the working hours.
Now, total cost is a function of W × T
Increase in wages = 20%
∴ Revised wages = 1.2 W
Decrease in labour time = (100/24)%
∴ Re vised time = (1-(1/24))T = (23/24)T
Re vised Total cost = 1.2 × (23/24)WT = 1.15WT
= 1.15 × 13200 = 15180
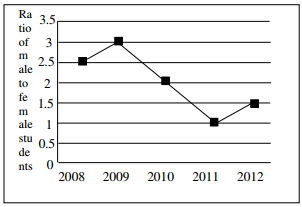
Q3. he ratio of male to female students in a college for five years is plotted in the following line
graph. If the number of female students in 2011 and 2012 is equal, what is the ratio of male
students in 2012 to male students in 2011?
Answer : Option C
Explaination / Solution:
Take number of female students in 2011=100
∴ Number of male in 2011=100
No. of female in 2012=100
No. of male in 2012=150
Ratio = 150/100 = 1.5:1
Q4. Let X and Y be finite sets and f : X → Y be a function. Which one of the following
statements is TRUE?
Answer : Option D
Explaination / Solution:
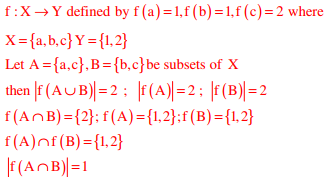
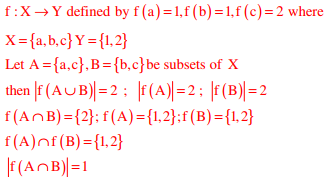
Q5. Which one of the following statements is TRUE about every n × n matrix with only real
eigenvalues?
Answer : Option A
Explaination / Solution:
If the trace of the matrix is positive and the determinant of the matrix is negative then atleast
one of its eigen values is negative.
Since determinant = product of eigen values.
Q6. Consider a hash table with 100 slots. Collisions are resolved using chaining. Assuming
simple uniform hashing, what is the probability that the first 3 slots are unfilled after the first
3 insertions?
Answer : Option A
Explaination / Solution:
Q7. With respect to the numerical evaluation of the definite integral,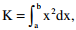 
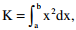where a and b
are given, which of the following statements is/are TRUE?
where a and b
are given, which of the following statements is/are TRUE?(I) The value of K obtained using the trapezoidal rule is always greater than or equal to the
exact value of the definite integral.
(II) The value of K obtained using the Simpson’s rule is always equal to the exact value of
the definite integral.
Answer : Option C
Explaination / Solution:
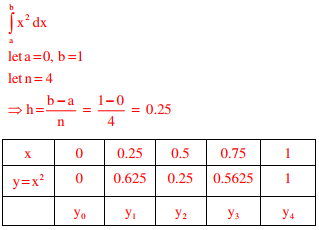
Q8. The value of the integral given below is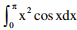 
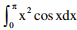
Answer : Option A
Explaination / Solution:
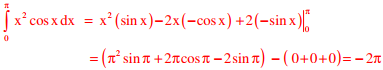
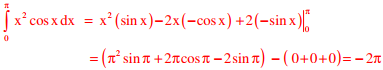
Q9. Consider the set of all functions f : {0,1,...,2014} → {0,1...,2014} such that f (f (i)) = i for 0 ≤ i ≤ 2014. Consider the following statements.
P. For each such function it must be the case that for every i, f(i) = i,
Q. For each such function it must be the case that for some i,f(i) = i,
R. Each such function must be onto.
Which one of the following is CORRECT?
Answer : Option B
Explaination / Solution:
No Explaination.
Q10. Let δ denote the minimum degree of a vertex in a graph. For all planar graphs on n vertices
with δ ≥3, which one of the following is TRUE?
Answer : Option A
Explaination / Solution:
We know that v + r = e+2 ⇒ e=n+r-2......(1)
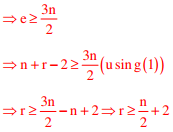
Where V= n (number of vertices); r = number of faces and
e = number of edges
Given, δ ≥ 3 then 3n ≤
2e
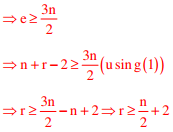
Number of faces is atleast (n/2) + 2
