Engineering Mathematics - Online Test
Q1. A deck of 5 cards (each carrying a distinct number from 1 to 5) is shuffled
thoroughly. Two cards are then removed one at a time from the deck. What is
the probability that the two cards are selected with the number on the first card
being one higher than the number on the second card?
Answer : Option A
Explaination / Solution:
(2,1), (3,2), (4,3), (5,4)
Required probability = 4/(5×4) = 4/20 = 1/5
Q2. If Log (P) = (1/2)Log (Q) = (1/3) Log (R), then which of the following options is
TRUE?
Answer : Option B
Explaination / Solution:
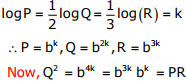
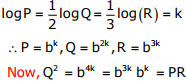
Q3. P, Q, R and S are four types of dangerous microbes recently found in a human
habitat. The area of each circle with its diameter printed in brackets represents
the growth of a single microbe surviving human immunity system within 24 hours
of entering the body. The danger to human beings varies proportionately with the
toxicity, potency and growth attributed to a microbe shown in the figure
below 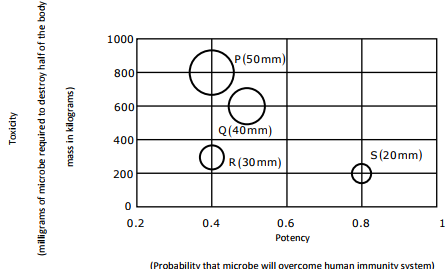

A pharmaceutical company is contemplating the development of a vaccine
against the most dangerous microbe. Which microbe should the company target
in its first attempt?
Answer : Option D
Explaination / Solution:
By observation of the table, we can say S


Q4. The variable cost (V) of manufacturing a product varies according to the equation
V= 4q, where q is the quantity produced. The fixed cost (F) of production of same
product reduces with q according to the equation F = 100/q. How many units
should be produced to minimize the total cost (V+F)?
Answer : Option A
Explaination / Solution:
Checking with all options in formula: (4q+100/q) i.e. (V+F). Option A gives the
minimum cost.
Q5. A container originally contains 10 litres of pure spirit. From this container 1 litre
of spirit is replaced with 1 litre of water. Subsequently, 1 litre of the mixture is
again replaced with 1 litre of water and this process is repeated one more time.
How much spirit is now left in the container?
Answer : Option D
Explaination / Solution:
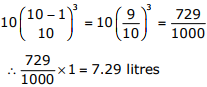
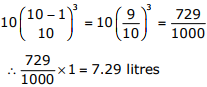
Q6. Consider a random variable X that takes values + 1 and -1 with probability 0.5 each. The
values of the cumulative distribution function F(x) at x = -1 and +1 are
Answer : Option C
Explaination / Solution:
The cumulative distribution function
F(x) = P(X ≤ x)
F(-1) = P(X ≤ -1) = P(X = -1) = 0.5
F(+1) = P(X ≤ +1) = P(X = -1) + P(X = +1) = 0.5 + 0.5 = 1
Q7. Let A be the 2 x 2 matrix with elements a11 = a12 = a21= + 1 and a22 =-1. Then the eigen values
of the matrix A19 are
Answer : Option D
Explaination / Solution:
Characteristic equation of A is |A - λI| = 0 where λ is the eigen value
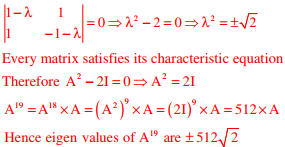
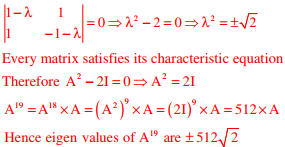
Q8. Consider the function f(x) = sin(x) in the interval x ∈ [π/4, 7π/4]. The number and location
(s) of the local minima of this function are
Answer : Option B
Explaination / Solution:
Sin x has a maximum value of 1 at , π/2 and a minimum value of –1 at 3π/2 and at all angles
conterminal with them.
The graph of f(x) = sin x is
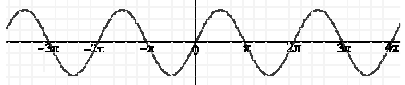

In the int erval [π/4, 7π/4], it has one local minimum at x = 3π/2
Q9. How many onto (or surjective) functions are there from an n-element (n ≥ 2) set to a 2-
element set?
Answer : Option C
Explaination / Solution:
Total number of functions is 2n , out of which there will be exactly two functions where all
elements map to exactly one element, so total number of onto functions is 2n -2
Q10. Suppose a fair six-sided die is rolled once. If the value on the die is 1, 2, or 3, the die is rolled
a second time. What is the probability that the sum total of values that turn up is at least 6?
Answer : Option B
Explaination / Solution:
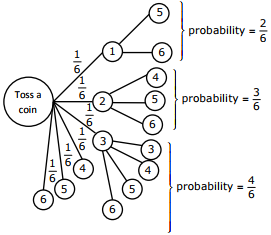

Required probability = 1/6 × 2/6 + 1/6 × 3/6 + 1/6 × 4/6 + 1/6 = 15/36 = 5/12
