Engineering Mathematics - Online Test
Q1. If 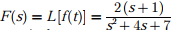 then the initial and final values of f(t) are
respectively
then the initial and final values of f(t) are
respectively
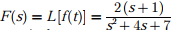 then the initial and final values of f(t) are
respectively
then the initial and final values of f(t) are
respectively
Answer : Option B
Explaination / Solution:
No Explaination.
Q2. A numerical solution of the equation 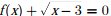 can be obtained using
Newton- Raphson method. If the starting value is x = 2 for the iteration, the
value of x that is to be used in the next step is
can be obtained using
Newton- Raphson method. If the starting value is x = 2 for the iteration, the
value of x that is to be used in the next step is
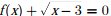 can be obtained using
Newton- Raphson method. If the starting value is x = 2 for the iteration, the
value of x that is to be used in the next step is
can be obtained using
Newton- Raphson method. If the starting value is x = 2 for the iteration, the
value of x that is to be used in the next step is
Answer : Option C
Explaination / Solution:
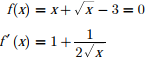
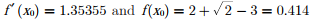
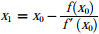
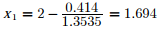
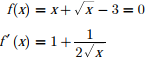
Substituting x0 = 2 we get
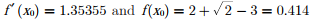
Newton Raphson Method
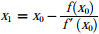
Substituting all values we have
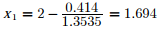
Q3. The system of equations
x + Y + z = 6
x + 4y + 6y = 20
x + 4y + λz = μ
has NO solution for values of λ and μ given by
Answer : Option B
Explaination / Solution:
Writing A:B we have

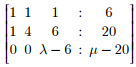

Apply R3⟶R3 – R2
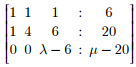
For equation to have solution, rank of A and A:B must be same. Thus for no
solution; λ = 6, μ ≠ 20
Q4. A fair dice is tossed two times. The probability that the second toss results in a value that is higher than the first toss is
Answer : Option C
Explaination / Solution:
Total outcome are 36 out of which favorable outcomes are :
(1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 3), (2, 4), (2, 5), (2, 6);
(3, 4), (3, 5), (3, 6), (4, 5), (4, 6), (5, 6) which are 15.
P(E) = (No of favourable outcomes/No of total outcomes) = 15/36
= 5/12
Q5. Three friends, R, S and T shared toffee from a bowl. R took 1/3rd of the toffees, but returned four to the bowl. S took 1/4th of what was left but returned three toffees to the bowl. T took half of the remainder but returned two back into the bowl. If the bowl had 17 toffees left, how many toffees-were originally there in the bowl?
Answer : Option C
Explaination / Solution:
Let total no of toffees be x . The following table shows the all calculations.
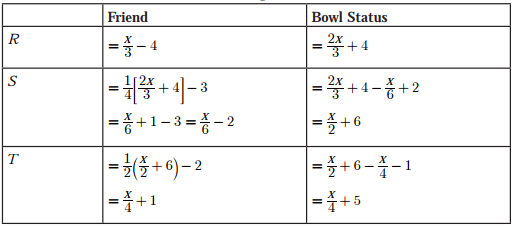
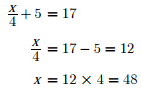

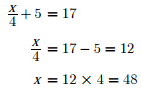
Q6. Given that 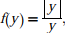 and q is any non-zero real number, the value
of |f(q) - f(-q)| is
and q is any non-zero real number, the value
of |f(q) - f(-q)| is
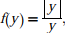 and q is any non-zero real number, the value
of |f(q) - f(-q)| is
and q is any non-zero real number, the value
of |f(q) - f(-q)| is
Answer : Option D
Explaination / Solution:
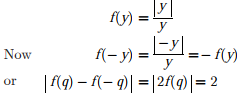
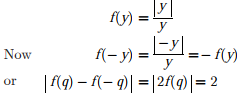
Q7. The sum of n terms of the series 4 + 44 + 444 + .... is
Answer : Option C
Explaination / Solution:
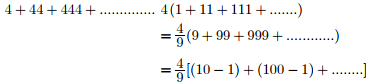
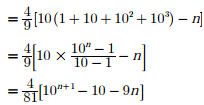
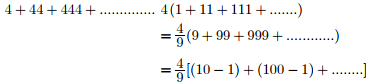
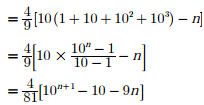
Q8. Let M4 = I, (where I denotes the identity matrix) and M ≠ I, M2 ≠ I and M3 ≠ I. Then, for any
natural number k, M-1 equals:
Answer : Option C
Explaination / Solution:


D is not correct
Q9. Given the following statements about a function
f : R⟶R, select the right option
P: If f(x) is continuous at x = x0, then it is also differentiable at x = x0.
Q: If f(x) is continuous at x = x0, then it may not be differentiable at x = x0.
R: If f(x) is differentiable at x = x0, then it is also continuous at x = x0.
Answer : Option B
Explaination / Solution:
We know that every differentiable function is continuous but converse need not be True
Q10. Which one of the following is a property of the solutions to the Laplace equation: Δ2f = 0?
Answer : Option A
Explaination / Solution:
No Explaination.
