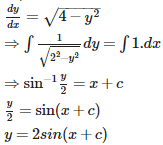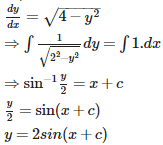Differential Equations - Online Test
Q1. Determine order and degree (if defined) ofcos() = 0
Answer : Option B
Explaination / Solution:
order = 2, degree not defined, because the function dy/dx present in angle of cosine function.
Q2. Determine order and degree (if defined) of
Answer : Option B
Explaination / Solution:
Order = 2 , degree = 1 .Since the highest derivative term is and its power is 1
Q3. What is the order of differential equation :
Answer : Option D
Explaination / Solution:
Order = 3.Since the third derivative is the highest derivative present in the equation. i.e.
Q4. Function y = f(x) is said to satisfy a differential equation g (y, y’, y’’...) =h(x) if
Answer : Option C
Explaination / Solution:
Function y = f(x) is said to satisfy a differential equation g (y, y’, y’’...) =h(x) if y and its derivatives substituted in equation g (y, y’, y’’...) =h(x) yield L.H.S. = R.H.S.
Q5. A function f(x,y) is said to be homogenous function of degree n if
Answer : Option C
Explaination / Solution:
A function is homogenous if we can write in the form of where n is an whole number .
Q6. General solution of a given differential equation
Answer : Option C
Explaination / Solution:
The general solution of differential equation contains arbitrary constants equal to the order of differential equaition.
Q7. Particular solution of a given differential equation
Answer : Option C
Explaination / Solution:
Particular solution of a given differential equation does not contain arbitrary constants i.e. a,b ,c etc since the value of those arbitrary can be found out by subsituting the given values.
Q8. The number of arbitrary constants in the general solution of a differential equation of fourth order are:
Answer : Option C
Explaination / Solution:
4 , because the no. of arbitrary constants is equal to order of the differential equation.
Q9. The number of arbitrary constants in the particular solution of a differential equation of third order are:
Answer : Option C
Explaination / Solution:
0 , because the particular solution is free from arbitrary constants.
Q10. General solution of ( -2 < y < 2) is
Answer : Option B
Explaination / Solution: