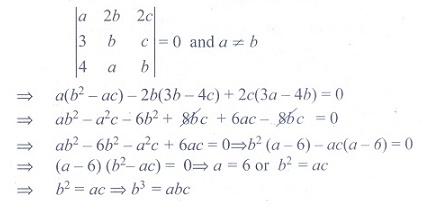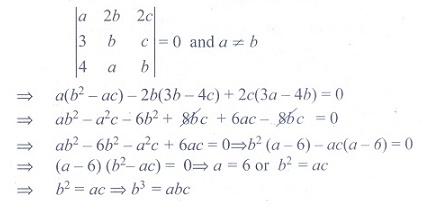Chapter 7: Matrices and Determinants - Online Test
Q1. The value of x, for which the matrix A = 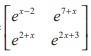 is singular is
is singular is
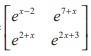 is singular is
is singular is
Answer : Option B
Explaination / Solution:
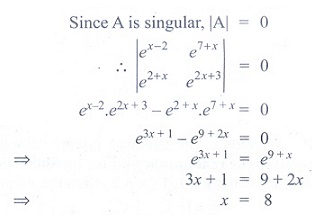
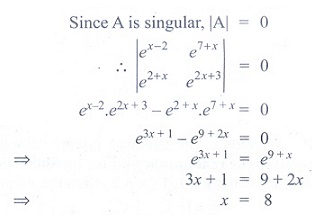
Q2. If the points (x, −2), (5, 2), (8,8) are collinear, then x is equal to
Answer : Option D
Explaination / Solution:


Q3. If 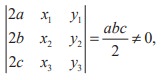 = abc/2
≠ 0, then the area of the triangle whose vertices are
= abc/2
≠ 0, then the area of the triangle whose vertices are 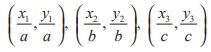 is
is
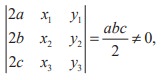 = abc/2
≠ 0, then the area of the triangle whose vertices are
= abc/2
≠ 0, then the area of the triangle whose vertices are 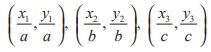 is
is
Answer : Option C
Explaination / Solution:


Q4. If the square of the matrix 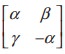 is the unit
matrix of order 2, then α, β and γ should satisfy the relation.
is the unit
matrix of order 2, then α, β and γ should satisfy the relation.
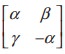 is the unit
matrix of order 2, then α, β and γ should satisfy the relation.
is the unit
matrix of order 2, then α, β and γ should satisfy the relation.
Answer : Option B
Explaination / Solution:
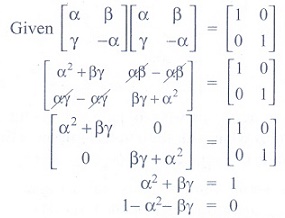
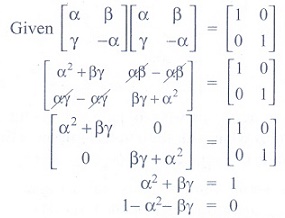
Q5. If 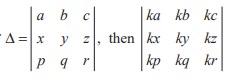 is
is
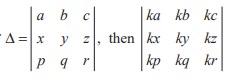 is
is
Answer : Option D
Explaination / Solution:
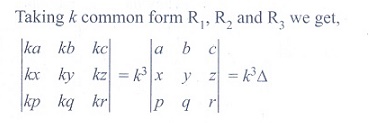
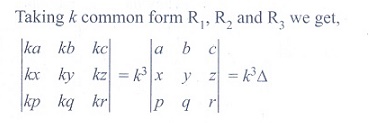
Q6. A root of the equation 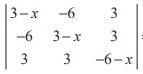 = 0 is
= 0 is
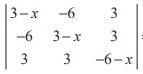 = 0 is
= 0 is
Answer : Option C
Explaination / Solution:


Q7. The value of the determinant of A = 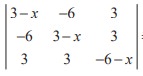 is
is
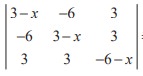 is
is
Answer : Option C
Explaination / Solution:
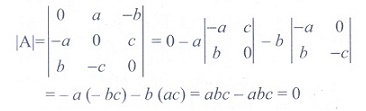
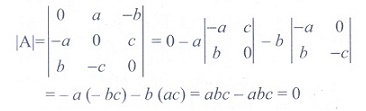
Q8. If x1
, x2 , x3 as well as y1 , y 2 , y3
are in geometric progression with the same common ratio, then the points (x1
, y1 ), (x2 , y2 ), (x3 , y3)
are
Answer : Option D
Explaination / Solution:


Q9. If 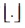 denotes the greatest integer less
than or equal to the real number under consideration and −1 ≤ x < 0, 0 ≤ y < 1, 1 ≤ z < 2 ,
then the value of the determinant
denotes the greatest integer less
than or equal to the real number under consideration and −1 ≤ x < 0, 0 ≤ y < 1, 1 ≤ z < 2 ,
then the value of the determinant 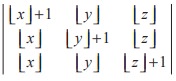 is
is
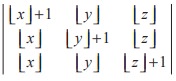 is
is
Answer : Option A
Explaination / Solution:
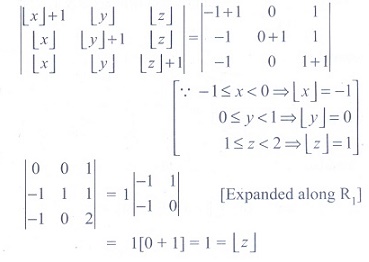
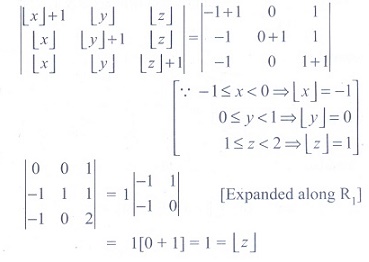
Q10. If a ≠ b, b, c satisfy 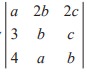 =
0, then abc =
=
0, then abc =
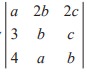 =
0, then abc =
=
0, then abc =
Answer : Option C
Explaination / Solution: