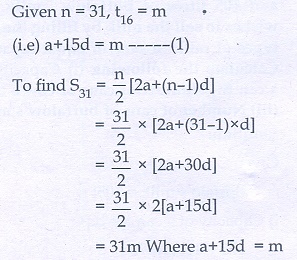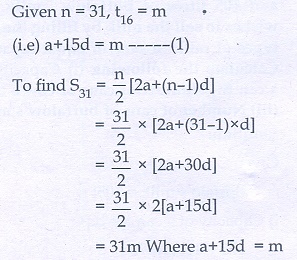Chapter 2: Numbers and Sequences - Online Test
Q1. Euclid’s division lemma
states that for positive integers a and b, there exist unique
integers q and r such that a = bq + r ,
where r must satisfy.
Answer : Option C
Explaination / Solution:
No Explaination.
Q2. Using Euclid’s division lemma, if the cube of any positive integer is divided by 9 then the possible remainders are
Answer : Option A
Explaination / Solution:


Q3. If the HCF of 65 and 117 is
expressible in the form of 65m -117 , then the value of m is
Answer : Option B
Explaination / Solution:


Q4. The sum of the exponents of the prime factors in the prime factorization of 1729 is
Answer : Option C
Explaination / Solution:
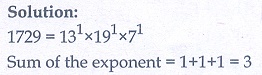
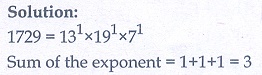
Q5. The least number that is divisible by all the numbers from 1 to 10 (both inclusive) is
Answer : Option D
Explaination / Solution:


Q6. 74k ≡
_____ (mod 100)
Answer : Option A
Explaination / Solution:


Q7. Given F1
= 1 , F2 = 3 and Fn = Fn−1
+ Fn−2 then F5 is
Answer : Option D
Explaination / Solution:
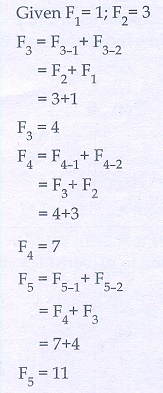
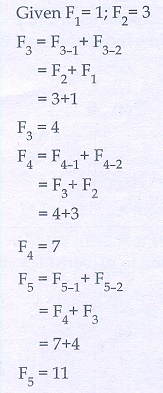
Q8. The first term of an arithmetic progression is unity and the common difference is 4. Which of the following will be a term of this A.P.
Answer : Option C
Explaination / Solution:


Q9. If 6 times of 6th
term of an A.P. is equal to 7 times the 7th term, then the 13th
term of the A.P. is
Answer : Option A
Explaination / Solution:
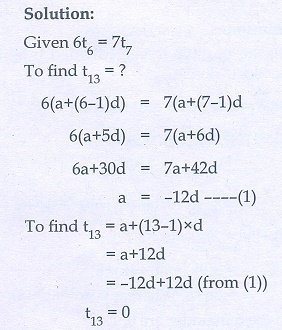
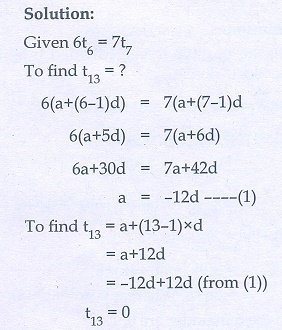
Q10. An A.P. consists of 31 terms. If its 16th term is m, then the sum of all the terms of this A.P. is
Answer : Option C
Explaination / Solution: