Chapter 12: Introduction to probability theory - Online Test
Q1. If A and B are two events such that A ⊂ B and P (B) ≠0, then which of the following is correct?
Answer : Option C
Explaination / Solution:
No Explaination.
Q2. A bag contains 6 green, 2 white, and 7 black balls. If two balls are drawn simultaneously, then the probability that both are different colours is
Answer : Option A
Explaination / Solution:


Q3. If X and Y be two events such that P ( X / Y ) = 1/2 , P ( Y / X ) = 1/3 and P ( X ∩ Y ) = 16 , then P ( X ∪Y ) is
Answer : Option D
Explaination / Solution:
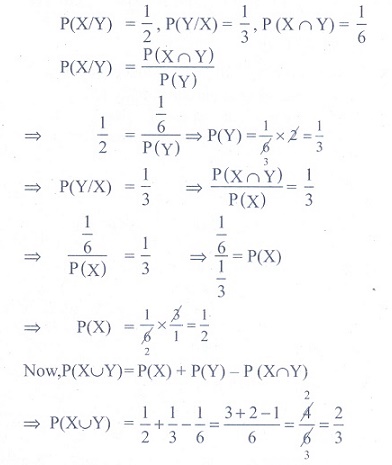
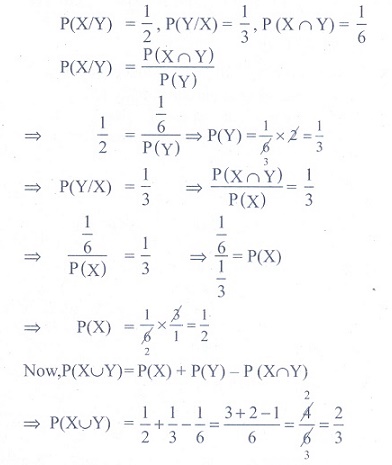
Q4. An urn contains 5 red and 5 black balls. A ball is drawn at random, its colour is noted and is returned to the urn. Moreover, 2 additional balls of the colour drawn are put in the urn and then a ball is drawn at random. The probability that the second ball drawn is red will be
Answer : Option B
Explaination / Solution:


Q5. A number x is chosen at random from the first 100 natural numbers. Let A be the event of numbers which satisfies [(x − 10)(x − 50)] / [x − 30 ] ≥ 0 , then P ( A) is
Answer : Option C
Explaination / Solution:


Q6. If two events A and B are independent such that P ( A) = 0.35 and P ( A ∪ B) = 0.6 , then P (B) is
Answer : Option A
Explaination / Solution:


Q7. If two events A and B are such that P (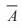 ) = 3/10 and P ( A ∩
) = 3/10 and P ( A ∩ 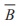 ) = 1/2 , then P ( A ∩ B) is
) = 1/2 , then P ( A ∩ B) is
Answer : Option D
Explaination / Solution:
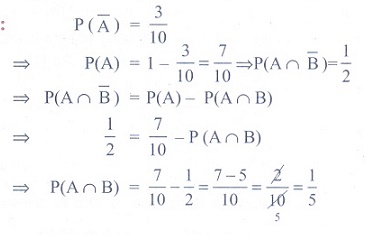
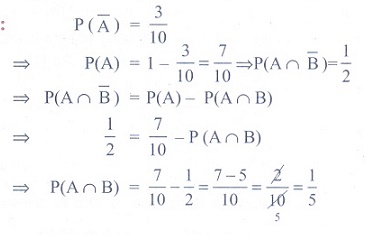
Q8. If A and B are two events such that P(A) = P ( B)
= and P ( B / A) = 0.6 , then P ( 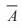 ∩ B) is
∩ B) is
Answer : Option C
Explaination / Solution:


Q9. There are three events A, B and C of which one and only one can happen. If the odds are 7 to 4 against A and 5 to 3 against B, then odds against C is
Answer : Option B
Explaination / Solution:


Q10. If a and b are chosen randomly from the set {1,2,3,4}with
replacement, then the probability of the real
roots of the equation x2 + ax + b = 0 is
Answer : Option C
Explaination / Solution:


