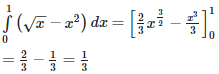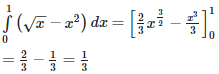Application of Integrals - Online Test
Q1. The area of the region between the curve y = 4 – and the x –axis is equal to
Answer : Option B
Explaination / Solution:
y = And
Required area:
= = =
Required area:
= = =
Q2. The area bounded by the curve and the x –axis is
Answer : Option B
Explaination / Solution:
The given curve consists of two straight lines x + y = 1 ( x ≥ 0 )and -x + y = 1 ( x < 0 )
Required area :
= = == = 1sq.unit
Required area :
= = == = 1sq.unit
Q3. The area enclosed by the curve is equal to
Answer : Option A
Explaination / Solution:
The area of the standard ellipse is given by ;πab. Here , a = 5 and b = 4 Therefore , the area of curve is π(5)(4)=20π.
Q4. The area of the curve is
Answer : Option C
Explaination / Solution:
Given equation is of a circle ; Its radius is equal to a. Therefore required area is =
Q5. The area bounded by the curve y = 4x - and the x- axis is equal to
Answer : Option C
Explaination / Solution:
For x – axis , y = 0,
Therefore,
Therefore , x = 0 or x = 4.
Required area :
= = = 32 - - 0 =
Therefore,
Therefore , x = 0 or x = 4.
Required area :
= = = 32 - - 0 =
Q6. The area bounded by the curve and y – axis is equal to
Answer : Option B
Explaination / Solution:
Required area :
= = =sq.units
Q7. The area bounded by y = log x , the x – axis and the ordinates x = 1 and x = 2 is
Answer : Option C
Explaination / Solution:
Required area :
= = == = = =
= = == = = =
Q8. Area bounded by the curves satisfying the conditions is given by
Answer : Option A
Explaination / Solution:
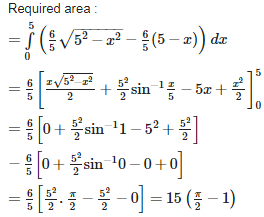
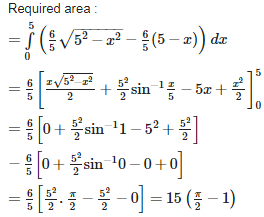
Q9. The area bounded by the parabola y = + 1 and the straight line x + y = 3 is given by
Answer : Option B
Explaination / Solution:
The two curves parabola and the line meet where,
3 - x = = 0
Required area ;
= =
3 - x = = 0
Required area ;
= =
Q10. The area bounded by the curves = x andy = is
Answer : Option A
Explaination / Solution:
The two curves meet in ( 0 , 0 ) and ( 1, 1 ).The required area lies above the curve y = x2 and below x = y2 and is equal to ;