Algorithms - Online Test
Q1. Let πA be a problem that belongs to the class NP. Then which one of the following is TRUE?
Answer : Option C
Explaination / Solution:
No Explaination.
Q2.
Consider the program below:
#include<stdio.h>
int fun (int n, int *fp)
{
int t, f;
if ( n<= 1)
{
*fp = 1;
return 1;
}
t = fun(n - 1, fp);
f = t+ * fp;
*fp = t;
return f;
}
int main( )
{
int x = 15;
printf (“%d\n”, fun (5, &x));
return 0;
}
The value printed is
Answer : Option B
Explaination / Solution:
No Explaination.
Q3. The running time of an algorithm is represented by the following recurrence relation:
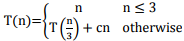
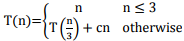
Which one of the following represents the time complexity of the algorithm?
Answer : Option A
Explaination / Solution:
No Explaination.
Q4. In quick sort, for sorting n elements, the (n/4)th the smallest element is selected as pivot using an O(n)
time algorithm. What is the worst case time complexity of the quick sort?
Answer : Option B
Explaination / Solution:
No Explaination.
Q5. What does the following program print?
#include <stdio.h>
void f (int * p, int * g) {
p = q;
* p = 2;
}
int i = 0, j = 1;
int main ( ){
f(&i, & j);
print f ("%d %d \ n", i, j);
return 0;
}
Answer : Option C
Explaination / Solution:
No Explaination.
Q6. What does the following fragment of C-program print?
char c[ ] = "GATE2011";
char *p =c;
printf ("%s", p+p[3] - p[1]);
Answer : Option C
Explaination / Solution:
No Explaination.
Q7. Consider the following recursive C function that takes two arguments
unsigned int foo unsigned int n, unsigned int r {
if (n > 0) return (n%r) + foo (n / r, r ));
else return 0;
}
What is the return value of the function foo when it is called as foo (513, 2)?
Answer : Option D
Explaination / Solution:
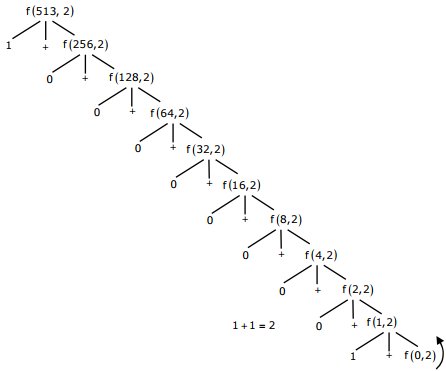

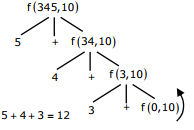
Q8. Consider the following recursive C function that takes two arguments
unsigned int foo unsigned int n, unsigned int r {
if (n > 0) return (n%r) + foo (n / r, r ));
else return 0;
}
What is the return value of the function foo when it is called as foo (345, 10) ?
Answer : Option B
Explaination / Solution:

Q9. Let W(n) and A(n) denote respectively, the worst case and average case running time of an
algorithm executed on an input of size n. Which of the following is ALWAYS TRUE?
Answer : Option C
Explaination / Solution:
The average case time can be lesser than or even equal to the worst case. So A(n) would be
upper bounded by W(n) and it will not be strict upper bound as it can even be same (e.g.
Bubble Sort and merge sort).
∴A(n) = O(W(n))
Q10. The recurrence relation capturing the optimal execution time of the Towers of Hanoi problem
with n discs is
Answer : Option D
Explaination / Solution:
Let the three pegs be A,B and C, the goal is to move n pegs from A to C using peg B
The following sequence of steps are executed recursively
1.move n−1 discs from A to B. This leaves disc n alone on peg A --- T(n-1)
2.move disc n from A to C---------1
3.move n−1 discs from B to C so they sit on disc n----- T(n-1)
So, T(n) = 2T(n-1) +1
