அலகு 6 : ஈர்ப்பியல் - Online Test
கோளின் நிலை வெக்டரும் நேர்க்கோட்டு உந்தமும் ஒன்றுக்கொன்று செங்குத்தாக அமைவது.
கோள்களின் பாதை நீள்வட்டப்பாதை, எனவே

திடீரென புவி மற்றும் சூரியனின் நிறைகள் இருமடங்காக மாறினால், அவைகளுக் கிடையேயான ஈர்ப்பியல் விசை
F = G Mm/r2
F’ = G [ 2M.2m / r2 ]
= 4[GMm/r2]
சூரியனை ஒரு கோள் நீள்வட்டப்பாதையில்
சுற்றி வருகிறது. கோளின் அண்மை தொலைவு (r1) மற்றும் சேய்மைத் தொலைவு (r2) களில் திசைவேகங்கள் முறையே v1 மற்றும் v2 எனில் v1/v2 =
கோண உந்தம் மாறாது.
L=rp=r(mv)=mvr
L1 = mv1r1 & L2 =
mv2 r2
L1 = L2
mv1 r1 = mv2 r2
V1 / V2 = r2 / r1 (∴ v ∝ 1 / r)
புவியினை வட்டப்பாதையில் சுற்றிவரும் துணைக் கோள்களின் சுற்றுக்காலம் எதனை சார்ந்தது அல்ல?
கெப்ளரின் சுற்றுக்கால விதிப்படி
T2 α r3 i.e. T2/r3 = மாறிலி
T = ஆரத்தைச் சார்ந்தது.
எனவே நிறையை சாராதது.
புவிக்கும் சூரியனுக்கும் இடையே உள்ள தொலைவு இருமடங்கானால் ஓராண்டு என்பது எத்தனை நாட்கள்

கெப்ளரின் இரண்டாம் விதிப்படி சூரியனையும் கோளையும் இணைக்கும் ஆர வெக்டர் சமகால அளவில் சமபரப்புகளை ஏற்படுத்துகின்றன. இவ்விதியானது ……. மாறாவிதிப்படி அமைந்துள்ளது.
புவியினைப் பொறுத்து நிலவின் ஈர்ப்புநிலை ஆற்றல்
புவியைப் பொருத்து நிலவின் ஈர்ப்பு
நிலை ஆற்றல் W = ‒GMm/r
(g க்கு எதிரே வேலை செய்வதால் v எதிர்க்குறி பெறும்)
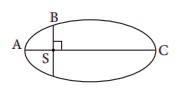
சூரியனை நீள்வட்டப்பாதையில் சுற்றிவரும் கோள் ஒன்று A, B மற்றும் C ஆகிய நிலைகளில் பெற்றுள்ள இயக்க ஆற்றல்கள் முறையே KA, Kb, மற்றும் Kc ஆகும். இங்கு நெட்டச்சு AC மற்றும் SB யானது சூரியனின் நிலை S‒ல் வரையப்படும் செங்குத்து எனில்,
KE = GmEmS / (RE + h)
KE ∝ 1 / Re↓
KA > KB > KC

புவியின் மீது சூரியனின் ஈர்ப்பியல் விசை செய்யும் வேலை
கெப்ளர் விதிப்படி, புவி சூரியனுக்கு
அருகில் ⇒ இ.ஆ. ↑
சூரியனுக்கு தொலைவில் ⇒ இ.ஆ. ↑
புவியின் நிறையும் ஆரமும் இரு மடங்கானால் ஈர்ப்பின் முடுக்கம் g
g = GM / R2
g = G(2M) / (2R)2 = 2GM / 4R2 =
1/2 (GM / R2)
g = g / 2