Ó«ģÓ«▓Ó«ĢÓ»ü 5 : Ó«żÓ»üÓ«ĢÓ«│Ó»ŹÓ«ĢÓ«│Ó«ŠÓ«▓Ó«ŠÓ«® Ó«ģÓ««Ó»łÓ«¬Ó»ŹÓ«¬Ó»ü Ó««Ó«▒Ó»ŹÓ«▒Ó»üÓ««Ó»Ź Ó«żÓ«┐Ó«ŻÓ»ŹÓ««Ó«¬Ó»ŹÓ«¬Ó»ŖÓ«░Ó»üÓ«¤Ó»ŹÓ«ĢÓ«│Ó«┐Ó«®Ó»Ź Ó«ćÓ«»Ó«ĢÓ»ŹÓ«ĢÓ««Ó»Ź - Online Test
Ó«żÓ»üÓ«ĢÓ«│Ó»ŹÓ«ĢÓ«│Ó«ŠÓ«▓Ó»Ź Ó«åÓ«® Ó«ģÓ««Ó»łÓ«¬Ó»ŹÓ«¬Ó«┐Ó«®Ó»Ź Ó«©Ó«┐Ó«▒Ó»ł Ó««Ó»łÓ«»Ó««Ó»Ź Ó«ÜÓ«ŠÓ«░Ó«ŠÓ«żÓ«┐Ó«░Ó»üÓ«¬Ó»ŹÓ«¬Ó«żÓ»ü
Ó«ćÓ«░Ó«¤Ó»ŹÓ«¤Ó»ł Ó«ēÓ«░Ó»üÓ«ĄÓ«ŠÓ«ĢÓ»ŹÓ«ĢÓ»üÓ«ĄÓ«żÓ»ü.
Ó«żÓ»üÓ«ÜÓ»ŹÓ«ÜÓ»üÓ«ĢÓ»ŹÓ«ĢÓ»ü Ó«åÓ«ÖÓ»ŹÓ«ĢÓ«┐Ó«ĢÓ»å Ó«ÄÓ«®Ó»Ź Ó«żÓ»üÓ«ĢÓ«│Ó»Ź Ó«ÆÓ«®Ó»ŹÓ«▒Ó»ü Ó««Ó«ŠÓ«▒Ó«ŠÓ«ż Ó«żÓ«┐Ó«ÜÓ»łÓ«ĄÓ»ćÓ«ĢÓ«żÓ»ŹÓ«żÓ»üÓ«¤Ó«®Ó»Ź
X Ó«ģÓ«ÜÓ»ŹÓ«ÜÓ»üÓ«ĢÓ»ŹÓ«ĢÓ»ü Ó«ćÓ«ŻÓ»łÓ«»Ó«ŠÓ«® Ó«©Ó»ćÓ«░Ó»ŹÓ«ĢÓ»ŹÓ«ĢÓ»ŗÓ«¤Ó»ŹÓ«¤Ó«┐Ó«®Ó»Ź Ó«ĄÓ«┤Ó«┐Ó«»Ó»ć Ó«ćÓ«»Ó«ÖÓ»ŹÓ«ĢÓ«┐ Ó«ĢÓ»ŖÓ«ŻÓ»ŹÓ«¤Ó«┐Ó«░Ó»üÓ«ĢÓ»ŹÓ«ĢÓ«┐Ó«▒Ó«żÓ»ü. Ó«åÓ«żÓ«┐Ó«»Ó»łÓ«¬Ó»Ź Ó«¬Ó»ŖÓ«░Ó»üÓ«żÓ»ŹÓ«żÓ»ü Ó«ÄÓ«ŻÓ»ŹÓ«ŻÓ«│Ó«ĄÓ«┐Ó«▓Ó»Ź Ó«ģÓ«żÓ«®Ó»Ź Ó«ĢÓ»ŗÓ«Ż Ó«ēÓ«©Ó»ŹÓ«żÓ««Ó»Ź.
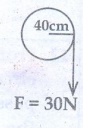
3 Kg Ó«©Ó«┐Ó«▒Ó»łÓ«»Ó»üÓ««Ó»Ź 40 cm Ó«åÓ«░Ó««Ó»üÓ««Ó»Ź Ó«ĢÓ»ŖÓ«ŻÓ»ŹÓ«¤ Ó«ēÓ«│Ó»ŹÓ«│Ó»ĆÓ«¤Ó«▒Ó»ŹÓ«▒ Ó«ēÓ«░Ó»üÓ«│Ó»łÓ«»Ó«┐Ó«®Ó»Ź Ó««Ó»ĆÓ«żÓ»ü Ó«ĢÓ«»Ó«┐Ó«▒Ó»ü Ó«ÆÓ«®Ó»ŹÓ«▒Ó»ü Ó«ÜÓ»üÓ«▒Ó»ŹÓ«▒Ó«¬Ó»ŹÓ«¬Ó«¤Ó»ŹÓ«¤Ó»üÓ«│Ó»ŹÓ«│Ó«żÓ»ü. Ó«ĢÓ«»Ó«┐Ó«▒Ó»ŹÓ«▒Ó»ł 30N Ó«ĄÓ«┐Ó«ÜÓ»łÓ«»Ó»ł Ó«ĢÓ»ŖÓ«ŻÓ»ŹÓ«¤Ó»ü Ó«ćÓ«┤Ó»üÓ«ĢÓ»ŹÓ«ĢÓ«¬Ó»ŹÓ«¬Ó«¤Ó»üÓ««Ó»Ź Ó«¬Ó»ŗÓ«żÓ»ü Ó«ēÓ«░Ó»üÓ«│Ó»łÓ«»Ó«┐Ó«®Ó»Ź Ó«ĢÓ»ŗÓ«Ż Ó««Ó»üÓ«¤Ó»üÓ«ĢÓ»ŹÓ«ĢÓ«żÓ»ŹÓ«żÓ»ł Ó«ĢÓ«ŠÓ«ŻÓ»ŹÓ«Ģ.
Žä = I╬▒ ;
F ├Ś R = MR2╬▒
30 ├Ś 0.4 = 3(0.4)2 ╬▒
12 = 3 ├Ś 0.16 ╬▒
400 = 16 ╬▒
╬▒ = 25 rad sŌĆÆ2
Ó«ēÓ«░Ó»üÓ«│Ó»ł Ó«ĄÓ«¤Ó«┐Ó«ĄÓ«ĢÓ»Ź Ó«ĢÓ«▓Ó«®Ó«┐Ó«▓Ó»Ź Ó«¬Ó«ĢÓ»üÓ«żÓ«┐Ó«»Ó«ŠÓ«Ģ Ó«©Ó»ĆÓ«░Ó»Ź Ó«©Ó«┐Ó«░Ó«¬Ó»ŹÓ«¬Ó«¬Ó»ŹÓ«¬Ó«¤Ó»ŹÓ«¤Ó»ü Ó««Ó»éÓ«¤Ó«┐ Ó«ĄÓ»łÓ«ĢÓ»ŹÓ«ĢÓ«¬Ó»ŹÓ«¬Ó«¤Ó»ŹÓ«¤Ó»üÓ«│Ó»ŹÓ«│Ó«żÓ»ü. Ó«ĢÓ«▓Ó«®Ó«┐Ó«▒Ó»ŹÓ«ĢÓ»ü Ó«ÜÓ»åÓ«ÖÓ»ŹÓ«ĢÓ»üÓ«żÓ»ŹÓ«żÓ»ü Ó«ćÓ«░Ó»ü Ó«ÜÓ«« Ó«ĄÓ»åÓ«¤Ó»ŹÓ«¤Ó«┐Ó«»Ó«┐Ó«®Ó»Ź Ó«ĄÓ«┤Ó«┐Ó«ÜÓ»ŹÓ«ÜÓ»åÓ«▓Ó»ŹÓ«▓Ó»üÓ««Ó»Ź Ó«ģÓ«ÜÓ»ŹÓ«ÜÓ»łÓ«¬Ó»ŹÓ«¬Ó«▒Ó»ŹÓ«▒Ó«┐ Ó«ĢÓ«┐Ó«¤Ó»łÓ«żÓ»Ź Ó«żÓ«│Ó«żÓ»ŹÓ«żÓ«┐Ó«▓Ó»Ź Ó«ÜÓ»üÓ«┤Ó«▓Ó»üÓ««Ó»Ź Ó«¬Ó»ŗÓ«żÓ»ü Ó«ģÓ«żÓ«®Ó»Ź Ó«©Ó«┐Ó«▓Ó»łÓ««Ó«żÓ»Ź Ó«żÓ«┐Ó«░Ó»üÓ«¬Ó»ŹÓ«¬Ó»üÓ«żÓ»ŹÓ«żÓ«┐Ó«▒Ó«®Ó»Ź.
Ó«żÓ«┐Ó«ŻÓ»ŹÓ«¬Ó»ŖÓ«░Ó»üÓ«│Ó»Ź Ó«ÆÓ«®Ó»ŹÓ«▒Ó»ü Ó«ĢÓ»ŗÓ«Ż Ó«ēÓ«©Ó»ŹÓ«żÓ««Ó»Ź L Ó«ēÓ«¤Ó«®Ó»Ź Ó«ÜÓ»üÓ«┤Ó«▓Ó»ŹÓ«ĢÓ«┐Ó«▒Ó«żÓ»ü Ó«ćÓ«żÓ«®Ó»Ź Ó«ćÓ«»Ó«ĢÓ»ŹÓ«Ģ Ó«åÓ«▒Ó»ŹÓ«▒Ó«▓Ó»Ź Ó«¬Ó«ŠÓ«żÓ«┐Ó«»Ó«ŠÓ«®Ó«ŠÓ«▓Ó»Ź Ó«ĢÓ»ŗÓ«Ż Ó«ēÓ«©Ó»ŹÓ«żÓ««Ó«ŠÓ«®Ó«żÓ»ü
L2 = 2I(KE) ;
KE = Ó«¬Ó«ŠÓ«żÓ«┐Ó«»Ó«ŠÓ«®Ó«ŠÓ«▓Ó»Ź
L2 = 2I (KE / 2)
L2 = 2I ├Ś [ L2 / 2I ] ├Ś [ 1/2 ]
L2 = L2 / 2
L = ŌłÜ[L2 / 2]
L = L / ŌłÜ2
Ó«żÓ»üÓ«ĢÓ«│Ó»Ź Ó«ÆÓ«®Ó»ŹÓ«▒Ó»ü Ó«ÜÓ»ĆÓ«░Ó«ŠÓ«® Ó«ĄÓ«¤Ó»ŹÓ«¤ Ó«ćÓ«»Ó«ĢÓ»ŹÓ«ĢÓ«żÓ»ŹÓ«żÓ«┐Ó«▒Ó»ŹÓ«ĢÓ»ü Ó«ēÓ«¤Ó»ŹÓ«¬Ó«¤Ó»üÓ«ĢÓ«┐Ó«▒Ó«żÓ»ü. Ó«ĢÓ»ŗÓ«Ż Ó«ēÓ«©Ó»ŹÓ«żÓ««Ó»Ź Ó«ÄÓ«żÓ»łÓ«¬Ó»Ź Ó«¬Ó»ŖÓ«░Ó»üÓ«żÓ»ŹÓ«żÓ»ü Ó««Ó«ŠÓ«▒Ó«ŠÓ«żÓ»ü
Ó«ÆÓ«░Ó»ü Ó«©Ó«┐Ó«▒Ó»łÓ«»Ó«ŠÓ«®Ó«żÓ»ü Ó«©Ó«┐Ó«▓Ó»łÓ«»Ó«ŠÓ«® Ó«¬Ó»üÓ«│Ó»ŹÓ«│Ó«┐Ó«»Ó»łÓ«¬Ó»Ź Ó«¬Ó»ŖÓ«░Ó»üÓ«żÓ»ŹÓ«żÓ»ü Ó«ÆÓ«░Ó»ü Ó«żÓ«│Ó«żÓ»ŹÓ«żÓ«┐Ó«▓Ó»Ź Ó«ÜÓ»üÓ«┤Ó«▓Ó»üÓ««Ó»Ź Ó«¬Ó»ŗÓ«żÓ»ü, Ó«ģÓ«żÓ«®Ó»Ź Ó«ĢÓ»ŗÓ«Ż Ó«ēÓ«©Ó»ŹÓ«żÓ«żÓ»ŹÓ«żÓ«┐Ó«®Ó»Ź Ó«żÓ«┐Ó«ÜÓ»łÓ«»Ó«ŠÓ«®Ó«żÓ»ü.
Ó«ÜÓ««Ó««Ó«ŠÓ«® Ó«©Ó«┐Ó«▓Ó»łÓ««Ó«żÓ»Ź Ó«żÓ«┐Ó«░Ó»üÓ«¬Ó»ŹÓ«¬Ó»üÓ«żÓ»ŹÓ«żÓ«┐Ó«▒Ó«®Ó»Ź Ó«ĢÓ»ŖÓ«ŻÓ»ŹÓ«¤ Ó«ĄÓ«¤Ó»ŹÓ«¤Ó«żÓ»ŹÓ«żÓ«¤Ó»ŹÓ«¤Ó»üÓ«ĢÓ«│Ó»Ź, Ó««Ó»łÓ«»Ó««Ó»Ź Ó«ĄÓ«┤Ó«┐Ó«»Ó»ć Ó«ĄÓ«¤Ó»ŹÓ«¤Ó«żÓ»ŹÓ«żÓ«¤Ó»ŹÓ«¤Ó»üÓ«ĢÓ«│Ó«┐Ó«®Ó»Ź Ó«żÓ«│Ó«żÓ»ŹÓ«żÓ«┐Ó«▒Ó»ŹÓ«ĢÓ»ü Ó«ÜÓ»åÓ«ÖÓ»ŹÓ«ĢÓ»üÓ«żÓ»ŹÓ«żÓ«ŠÓ«Ģ Ó«ÜÓ»åÓ«▓Ó»ŹÓ«▓Ó»üÓ««Ó»Ź Ó«ģÓ«ÜÓ»ŹÓ«ÜÓ»łÓ«¬Ó»Ź Ó«¬Ó«▒Ó»ŹÓ«▒Ó«┐ Žē1, Ó««Ó«▒Ó»ŹÓ«▒Ó»üÓ««Ó»Ź Žē2 Ó«ÄÓ«®Ó»ŹÓ«▒ Ó«ĢÓ»ŗÓ«Ż Ó«żÓ«┐Ó«ÜÓ»łÓ«ĄÓ»ćÓ«ĢÓ«ÖÓ»ŹÓ«ĢÓ«│Ó»üÓ«¤Ó«®Ó»Ź Ó«ÜÓ»üÓ«┤Ó«▓Ó»ŹÓ«ĢÓ«┐Ó«®Ó»ŹÓ«▒Ó«®. Ó«ćÓ«ĄÓ»ŹÓ«ĄÓ«┐Ó«░Ó»ü Ó«ĄÓ«¤Ó»ŹÓ«¤Ó«żÓ»ŹÓ«żÓ«¤Ó»ŹÓ«¤Ó»üÓ«ĢÓ«│Ó«┐Ó«®Ó»Ź Ó«ģÓ«ÜÓ»ŹÓ«ÜÓ»üÓ«ĢÓ«│Ó»ł Ó«ÆÓ«®Ó»ŹÓ«▒Ó«┐Ó«ŻÓ»łÓ«ĢÓ»ŹÓ«ĢÓ»üÓ««Ó«ŠÓ«▒Ó»ü
Ó«ģÓ«ĄÓ»ł Ó«ÆÓ«®Ó»ŹÓ«▒Ó»üÓ«¤Ó«®Ó»Ź Ó«ÆÓ«®Ó»ŹÓ«▒Ó»ü Ó«¬Ó»ŖÓ«░Ó»üÓ«żÓ»ŹÓ«żÓ«¬Ó»ŹÓ«¬Ó«¤Ó»üÓ«ĢÓ«┐Ó«®Ó»ŹÓ«▒Ó«® Ó«ÄÓ«®Ó«┐Ó«▓Ó»Ź, Ó«ćÓ«©Ó»ŹÓ«©Ó«┐Ó«ĢÓ«┤Ó»ŹÓ«ĄÓ«┐Ó«®Ó»Ź Ó«¬Ó»ŗÓ«żÓ»ü Ó«åÓ«▒Ó»ŹÓ«▒Ó«▓Ó»Ź Ó«ćÓ«┤Ó«¬Ó»ŹÓ«¬Ó«┐Ó«▒Ó»ŹÓ«ĢÓ«ŠÓ«® Ó«ĢÓ»ŗÓ«ĄÓ»łÓ«»Ó«ŠÓ«®Ó«żÓ»ü.
I1=I2=I
Δ KE = 1/2 ([I1 I2] /
[I1 + I2]) (Žē1 ŌĆō
Žē2)2
= 1/2 (I 2 / (2I))
(Žē1 ŌĆō Žē2)2
= 1/4 I (Žē1 ŌĆō Žē2)2
Ia Ó«©Ó«┐Ó«▓Ó»łÓ««Ó«żÓ»Ź Ó«żÓ«┐Ó«░Ó»üÓ«¬Ó»ŹÓ«¬Ó»üÓ«żÓ»ŹÓ«żÓ«┐Ó«▒Ó«®Ó»Ź
Ó«ĢÓ»ŖÓ«ŻÓ»ŹÓ«¤ Ó«ĄÓ«¤Ó»ŹÓ«¤Ó«żÓ»ŹÓ«żÓ«¤Ó»ŹÓ«¤Ó»ü Ó««Ó«ŠÓ«▒Ó«ŠÓ«ż Ó«ĢÓ»ŗÓ«Ż Ó«żÓ«┐Ó«ÜÓ»łÓ«ĄÓ»ćÓ«ĢÓ««Ó»Ź Žē Ó«ĄÓ»üÓ«¤Ó«®Ó»Ź Ó«ĢÓ«┐Ó«¤Ó»łÓ«żÓ»ŹÓ«żÓ«│Ó«żÓ»ŹÓ«żÓ«┐Ó«▓Ó»Ź Ó«ÜÓ««Ó«ÜÓ»ŹÓ«ÜÓ»ĆÓ«░Ó«ŠÓ«® Ó«ģÓ«ÜÓ»ŹÓ«ÜÓ»łÓ«¬Ó»Ź Ó«¬Ó«▒Ó»ŹÓ«▒Ó«┐ Ó«ÜÓ»üÓ«┤Ó«▓Ó»ŹÓ«ĢÓ«┐Ó«▒Ó«żÓ»ü. Ó«ōÓ«»Ó»ŹÓ«ĄÓ»ü Ó«©Ó«┐Ó«▓Ó»łÓ«»Ó«┐Ó«▓Ó»üÓ«│Ó»ŹÓ«│ Ó««Ó«▒Ó»ŹÓ«▒Ó»ŖÓ«░Ó»ü Ó«ĄÓ«¤Ó»ŹÓ«¤Ó«żÓ»ŹÓ«żÓ«¤Ó»ŹÓ«¤Ó«┐Ó«®Ó»Ź Ib Ó«ÄÓ«®Ó»ŹÓ«▒ Ó«©Ó«┐Ó«▓Ó»łÓ««Ó«żÓ»ŹÓ«żÓ«┐Ó«░Ó»üÓ«¬Ó»ŹÓ«¬Ó»üÓ«żÓ»ŹÓ«żÓ«┐Ó«▒Ó«®Ó»üÓ«¤Ó«®Ó»Ź Ó«ÜÓ»üÓ«┤Ó«▓Ó»üÓ««Ó»Ź Ó«ĄÓ«¤Ó»ŹÓ«¤Ó«żÓ»ŹÓ«żÓ«¤Ó»ŹÓ«¤Ó«┐Ó«®Ó»Ź
Ó««Ó»ĆÓ«żÓ»ü Ó«ģÓ«ÜÓ»ŹÓ«ÜÓ»üÓ«┤Ó«▓Ó»üÓ««Ó»Ź Ó«ģÓ«ÜÓ»ŹÓ«ÜÓ«┐Ó«▓Ó»ćÓ«»Ó»ć Ó«ĄÓ«┐Ó«¤Ó«¬Ó»ŹÓ«¬Ó«¤Ó»üÓ«ĢÓ«┐Ó«▒Ó«żÓ»ü. Ó«ćÓ«żÓ«®Ó«ŠÓ«▓Ó»Ź Ó«ćÓ«░Ó»ü Ó«ĄÓ«¤Ó»ŹÓ«¤Ó«żÓ»ŹÓ«żÓ«żÓ«¤Ó»ŹÓ«¤Ó»üÓ«ĢÓ«│Ó»üÓ««Ó»Ź Ó««Ó«ŠÓ«▒Ó«Š Ó«ĢÓ»ŗÓ«Ż Ó«ĄÓ»ćÓ«ĢÓ«żÓ»ŹÓ«żÓ«┐Ó«▓Ó»Ź Ó«ÜÓ»üÓ«┤Ó«▓Ó»ŹÓ«ĢÓ«┐Ó«▒Ó«żÓ»ü. Ó«ćÓ«©Ó»ŹÓ«©Ó«┐Ó«ĢÓ«┤Ó»ŹÓ«ĄÓ«┐Ó«▓Ó»Ź Ó«ēÓ«░Ó«ŠÓ«»Ó»ŹÓ«ĄÓ«┐Ó«®Ó«ŠÓ«▓Ó»Ź Ó«ÅÓ«▒Ó»ŹÓ«¬Ó«¤Ó»üÓ««Ó»Ź Ó«åÓ«▒Ó»ŹÓ«▒Ó«▓Ó»Ź Ó«ćÓ«┤Ó«¬Ó»ŹÓ«¬Ó»ü.
Li = Lf
IaŽēa = IfŽēf
IaŽēa = (Ia+Ib)Žēf