அலகு 2 : இயக்கவியல் - Online Test
பின்வரும் எந்த கார்டீசியன் ஆய அச்சுத் தொகுப்பு இயற்பியலில் பயன்படுத்தப்படுவதில்லை.
இயற்பியலில் ஆய அச்சின் திசை கடிகார முள் சுழலும் திசைக்கு எதிர் திசை கருத்தில் கொள்ளப்படும். (a), (b), (c) அவ்வாறு உள்ளது.
d) மட்டும் கடிகார முள் திசையில் உள்ளது
பின்வருவனவற்றுள்
எது ஓரலகு வெக்டர்?
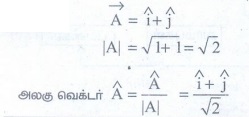
பின்வருவனவற்றுள்
எந்த இயற்பியல் அளவு ஸ்கேலரால் குறிப்பிட இயலாது?
m1 மற்றும் m2 நிறை கொண்ட இரண்டு பொருட்கள் h1 மற்றும் h2 உயரத்திலிருந்து விழுகின்றன. அவை தரையை அடையும்போது அவற்றின் உந்தங்களின் எண்மதிப்புகளின்
விகிதம் என்ன?
தரையை அடையும் போது பெரும் அளவு v2 = 2gh
=> v = √[2gh],
p = mv = m √[2gh]
p1 ∝ m1√h1
p2 ∝ m2√h2
p1/p2 = m2/m1 √[h1/h2]
துகளொன்று எதிர்குறி திசைவேகத்தையும், எதிர்குறி முடுக்கத்தையும் பெற்றுள்ளது எனில், அத்துகளின் வேகம்
v = ‒v எனில் a = ‒v/t
திசைவேகத்தின்
எண் மதிப்பு வேகம்
ஃ வேகம் |(‒v)| = v அதிகரிக்கும்
துகளொன்றின் திசைவேகம்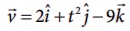 
, எனில், t = 0.5 வினாடியில் அத்துகளின் முடுக்கத்தின் எண்மதிப்பு யாது?
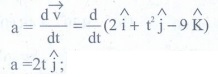
பொருளொன்று கட்டிடத்தின் உச்சியிலிருந்து கீழே விழுகிறது, அப்பொருள் 4 வினாடியில் தரையை அடைந்தால் கட்டிடத்தின் உயரமென்ன? (காற்றுத்தடையைப் ‒ புறக்கணிக்க)
s = ut + ½ gt2; u= 0
s = gt2 / 2 = [9.8×4 ×4] / 2 = 78.4m
v என்ற திசைவேகத்துடன்
பந்து ஒன்று செங்குத்தாக மேல்நோக்கி எறியப்படுகிறது
அது t நேரத்தில் தரையை அடைகிறது. பின்வரும் எந்த v‒t வரைபடம் இவ்வியக்கத்தினை
சரியாக விளக்குகிறது.
பந்து செங்குத்தாக எறியும் போது பெரும் உயரத்தை அடையும் வரை திசைவேகம் குறைந்து கொண்டே செல்லும். பின் எதிர்த் திசையில் அதிகரிக்கும். (தரையை நோக்கி) இந்த நிபந்தனை (c)க்கு பொருந்தும்.
சம உயரத்தில் உள்ள இரு பொருட்களில் ஒன்று தானாக கீழ்நோக்கி விழுகிறது. மற்றொன்று கிடைத்தளத்தில் எறியப்படுகிறது. 't' வினாடியில் அவை கடந்த செங்குத்து தொலைவுகளின் விகிதம் என்ன?
இரு பொருள்களுக்கும் உயரம் சமம் எனவே g சமம்.
h = 1/2 gt2;
t = √(2h / g)
h1/h2 = 1
குறிப்பிட்ட உயரத்திலிருந்து பந்து ஒன்று கீழே விழுகிறது. பின்வருவனவற்றுள்
எப்படம் பந்தின் இயக்கத்தினைச் சரியாக விளக்குகிறது?
