Я«ЁЯ«▓Я«ЋЯ»Ђ 12 : Я«еЯ«┐Я«ЋЯ«┤Я»ЇЯ«цЯ«ЋЯ«хЯ»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ Я«ЊЯ«░Я»Ї Я«ЁЯ«▒Я«┐Я««Я»ЂЯ«ЋЯ««Я»Ї - Online Test
A Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї B Я«єЯ«ЋЯ«┐Я«» Я«ЄЯ«░Я»Ђ Я«еЯ«┐Я«ЋЯ«┤Я»ЇЯ«џЯ»ЇЯ«џЯ«┐Я«ЋЯ«│Я»Ї A Ріѓ B Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї P(B) РЅа 0, Я«јЯ«Е Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ«хЯ«ЕЯ«хЯ«▒Я»ЇЯ«▒Я»ЂЯ«│Я»Ї Я«јЯ«цЯ»Ђ Я««Я»єЯ«»Я»ЇЯ«»Я«ЙЯ«ЕЯ«цЯ»Ђ?
Я«њЯ«░Я»Ђ Я«фЯ»ѕЯ«»Я«┐Я«▓Я»Ї 6 Я«фЯ«џЯ»ЇЯ«џЯ»ѕ, 2 Я«хЯ»єЯ«│Я»ЇЯ«│Я»ѕ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 7Я«ЋЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«еЯ«┐Я«▒ Я«фЯ«еЯ»ЇЯ«цЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«Е. Я«ЄЯ«░Я»Ђ Я«фЯ«еЯ»ЇЯ«цЯ»ЂЯ«ЋЯ«│Я»Ї Я«њЯ«░Я»Є Я«џЯ««Я«»Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«јЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«ЁЯ«хЯ»ѕ Я«хЯ»єЯ«хЯ»ЇЯ«хЯ»ЄЯ«▒Я»Ђ Я«еЯ«┐Я«▒Я««Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ«▒Я»ЇЯ«ЋЯ«ЙЯ«Е Я«еЯ«┐Я«ЋЯ«┤Я»ЇЯ«цЯ«ЋЯ«хЯ«ЙЯ«ЕЯ«цЯ»Ђ

X Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Y Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЄЯ«░Я»Ђ Я«еЯ«┐Я«ЋЯ«┤Я»ЇЯ«џЯ»ЇЯ«џЯ«┐Я«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ P(X/Y) =
1/2, P(Y/X) = 1/3, P(XРѕЕY) = 1/6 Я«јЯ«ЕЯ«┐Я«▓Я»Ї P(XРѕфY) РђњЯ«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ

Я«њЯ«░Я»Ђ Я«юЯ«ЙЯ«ЪЯ«┐Я«»Я«┐Я«▓Я»Ї 5 Я«џЯ«┐Я«хЯ«фЯ»ЇЯ«фЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 5 Я«ЋЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«еЯ«┐Я«▒ Я«фЯ«еЯ»ЇЯ«цЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«Е. Я«юЯ«ЙЯ«ЪЯ«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«џЯ««Я«хЯ«ЙЯ«»Я»ЇЯ«фЯ»ЇЯ«фЯ»Ђ Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«њЯ«░Я»Ђ Я«фЯ«еЯ»ЇЯ«цЯ»Ђ Я«јЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЁЯ«цЯ«ЕЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я«еЯ«┐Я«▒Я««Я»ЂЯ«│Я»ЇЯ«│ Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я«ЄЯ«░Я»Ђ Я«фЯ«еЯ»ЇЯ«цЯ»ЂЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«юЯ«ЙЯ«ЪЯ«┐Я«»Я«┐Я«▓Я»Ї Я««Я»ђЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«хЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ«░Я»Ї Я«юЯ«ЙЯ«ЪЯ«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«фЯ«еЯ»ЇЯ«цЯ»Ђ Я«јЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«ЁЯ«цЯ»Ђ Я«џЯ«┐Я«хЯ«фЯ»ЇЯ«фЯ»Ђ Я«еЯ«┐Я«▒Я«фЯ»Ї Я«фЯ«еЯ»ЇЯ«цЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ«▒Я»ЇЯ«ЋЯ«ЙЯ«Е Я«еЯ«┐Я«ЋЯ«┤Я»ЇЯ«цЯ«ЋЯ«хЯ«ЙЯ«ЕЯ«цЯ»Ђ

Я«њЯ«ЕЯ»ЇЯ«▒Я»Ђ Я««Я»ЂЯ«цЯ«▓Я»Ї Я«еЯ»ѓЯ«▒Я»Ђ Я«хЯ«░Я»ѕЯ«»Я»ЂЯ«│Я»ЇЯ«│ Я«ЄЯ«»Я«▓Я»Ї Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«џЯ««Я«хЯ«ЙЯ«»Я»ЇЯ«фЯ»ЇЯ«фЯ»Ђ Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«њЯ«░Я»Ђ Я«јЯ«БЯ»Ї x Я«цЯ»ЄЯ«░Я»ЇЯ«еЯ»ЇЯ«цЯ»єЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. 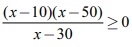 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЕЯ»ѕЯ«фЯ»Ї Я«фЯ»ѓЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ«┐ Я«џЯ»єЯ«»Я»ЇЯ«»Я»ЂЯ««Я»Ї Я«јЯ«БЯ»ЇЯ«БЯ»ѕЯ«цЯ»Ї Я«цЯ»ЄЯ«░Я»ЇЯ«хЯ»Ђ Я«џЯ»єЯ«»Я»ЇЯ«»Я»ЂЯ««Я»Ї Я«еЯ«┐Я«ЋЯ«┤Я»ЇЯ«џЯ»ЇЯ«џЯ«┐ A Я«јЯ«ЕЯ«┐Я«▓Я»Ї, P(A) Я«єЯ«ЕЯ«цЯ»Ђ
Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЕЯ»ѕЯ«фЯ»Ї Я«фЯ»ѓЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ«┐ Я«џЯ»єЯ«»Я»ЇЯ«»Я»ЂЯ««Я»Ї Я«јЯ«БЯ»ЇЯ«БЯ»ѕЯ«цЯ»Ї Я«цЯ»ЄЯ«░Я»ЇЯ«хЯ»Ђ Я«џЯ»єЯ«»Я»ЇЯ«»Я»ЂЯ««Я»Ї Я«еЯ«┐Я«ЋЯ«┤Я»ЇЯ«џЯ»ЇЯ«џЯ«┐ A Я«јЯ«ЕЯ«┐Я«▓Я»Ї, P(A) Я«єЯ«ЕЯ«цЯ»Ђ

A Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї B Я«јЯ«ЕЯ»ЇЯ«▒ Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ«┐Я«▓Я«Й Я«еЯ«┐Я«ЋЯ«┤Я»ЇЯ«џЯ»ЇЯ«џЯ«┐Я«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ P(A) = 0.35 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї P(AРѕфB) = 0.6, Я«јЯ«ЕЯ«┐Я«▓Я»Ї P(B) Я«єЯ«ЕЯ«цЯ»Ђ

A Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї B Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЄЯ«░Я»Ђ Я«еЯ«┐Я«ЋЯ«┤Я»ЇЯ«џЯ»ЇЯ«џЯ«┐Я«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ 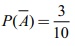 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї
Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї  , Я«јЯ«ЕЯ«┐Я«▓Я»Ї P(AРѕЕB)РђњЯ«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ
, Я«јЯ«ЕЯ«┐Я«▓Я»Ї P(AРѕЕB)РђњЯ«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ
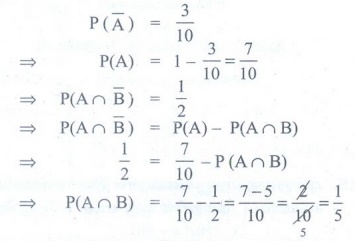
A Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї B Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЄЯ«░Я»Ђ Я«еЯ«┐Я«ЋЯ«┤Я»ЇЯ«џЯ»ЇЯ«џЯ«┐Я«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ P(A) = 0.4, P(B) = 0.8 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї P(B/A) = 0.6, Я«јЯ«ЕЯ«┐Я«▓Я»Ї 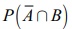 РђњЯ«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ
РђњЯ«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ

A, B Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї C Я«јЯ«ЕЯ»ЇЯ«▒ Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«еЯ«┐Я«ЋЯ«┤Я»ЇЯ«џЯ»ЇЯ«џЯ«┐Я«ЋЯ«│Я«┐Я«▓Я»Ї Я«њЯ«ЕЯ»ЇЯ«▒Я»Ђ Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Є Я«еЯ«┐Я«ЋЯ«┤Я«ЋЯ»ЇЯ«ЋЯ»ѓЯ«ЪЯ»ЂЯ««Я»Ї. AРђњЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«џЯ«ЙЯ«цЯ«ЋЯ««Я«▒Я»ЇЯ«▒ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»Ї 7 РђњЯ«ЋЯ»ЇЯ«ЋЯ»Ђ 4 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї B РђњЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«џЯ«ЙЯ«цЯ«ЋЯ««Я«▒Я»ЇЯ«▒ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»Ї 5 РђњЯ«ЋЯ»ЇЯ«ЋЯ»Ђ 3 Я«јЯ«ЕЯ«┐Я«▓Я»Ї C РђњЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ«ЙЯ«цЯ«ЋЯ««Я«▒Я»ЇЯ«▒ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»Ї

a Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї bРђњЯ«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї {1,2,3,4} Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«цЯ«┐Я«░Я»ЂЯ««Я»ЇЯ«фЯ«цЯ»Ї Я«цЯ«┐Я«░Я»ЂЯ««Я»ЇЯ«ф Я«хЯ«░Я»ЂЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«▒ Я«хЯ«ЋЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«џЯ««Я«хЯ«ЙЯ«»Я»ЇЯ«фЯ»ЇЯ«фЯ»Ђ Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«цЯ»ЄЯ«░Я»ЇЯ«еЯ»ЇЯ«цЯ»єЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«▓Я»Ї x2 + ax + b= 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»ЇЯ«ЋЯ«│Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ«▒Я»ЇЯ«ЋЯ«ЙЯ«Е Я«еЯ«┐Я«ЋЯ«┤Я»ЇЯ«цЯ«ЋЯ«хЯ»Ђ