CBSE 12TH MATHEMATICS - Online Test
Q1. The area bounded by the curve y = , the x – axis and two ordinates x = 1 and x = 2 is
Answer : Option B
Explaination / Solution:
sq.units.
Q2. A square matrix is called a diagonal matrix if for
Answer : Option B
Explaination / Solution:
In a diagonal matrix all elements except diagonal elements are zero.i.e.
Q3.
The function f (x) = , for all real x, is
Answer : Option A
Explaination / Solution:
f(x) = x2
f'(x) = 2x for all x in R.
Since f ‘(x) = 2x > 0 for x >0, and f ‘ (x) = 2x< 0 for x < 0 ,therefore on R , f is neither increasing nor decreasing . Infact , f is strict increasing on [ 0 , ) and strict decreasing on (- ].
f'(x) = 2x for all x in R.
Since f ‘(x) = 2x > 0 for x >0, and f ‘ (x) = 2x< 0 for x < 0 ,therefore on R , f is neither increasing nor decreasing . Infact , f is strict increasing on [ 0 , ) and strict decreasing on (- ].
Q4. One root of the equation 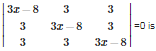
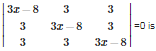
Answer : Option D
Explaination / Solution:


Q5. Let R be the feasible region for a linear programming problem, and let Z = ax + by be the objective function. If R is bounded, then
Answer : Option A
Explaination / Solution:
Let R be the feasible region for a linear programming problem, and let Z = ax + by be the objective function. If R is bounded, then the objective function Z has both a maximum and a minimum value on R and each of these occur at the corner point (vertex) of R.
Q6. R = {(1, 1), (2, 2), (1, 2), (2, 1), (2, 3)} be a relation on A, then R is
Answer : Option B
Explaination / Solution:
A relation R on a non empty set A is said to be reflexive if xRx for all x R , Therefore , R is not reflexive.
A relation R on a non empty set A is said to be symmetric if xRyyRx, for all x , y R Therefore, R is not symmetric.
A relation R on a non empty set A is said to be antisymmetric if xRy and yRxx = y , for all x , y R.Therefore, R is not antisymmetric.
A relation R on a non empty set A is said to be symmetric if xRyyRx, for all x , y R Therefore, R is not symmetric.
A relation R on a non empty set A is said to be antisymmetric if xRy and yRxx = y , for all x , y R.Therefore, R is not antisymmetric.
Q7. is equal to
Answer : Option A
Explaination / Solution:
Note that is an odd function, therefore,
Q8. Unit Vector is
Answer : Option D
Explaination / Solution:
The vector whose magnitude is always 1 or unity is called a Unit Vector.
Q9. If P(A) = , P(B) = 0, then P(A|B) is
Answer : Option D
Explaination / Solution:
We know that :
which is not defined
which is not defined
Q10. When x=,x/2,then tan x, is
Answer : Option B
Explaination / Solution:
tan(π2)=sin(π2)cos(π2)=10=notdefined
