CBSE 12TH MATHEMATICS - Online Test
Q1. Let A and B be independent events with P (A) = 0.3 and P(B) = 0.4. Find P(A ∩ B)
Answer : Option B
Explaination / Solution:
Let A and B be independent events with P (A) = 0.3 and P(B) = 0.4
Q2. Let A and B be independent events with P (A) = 0.3 and P(B) = 0.4.Find P(A ∪ B)
Answer : Option C
Explaination / Solution:
Let A and B be independent events with P (A) = 0.3 and P(B) = 0.4
Since the events are independent, P(AB) = P(A).P(B)
ThereforeP(AB) = P(A) + P(B)
= 0.3 + 0.4 - 0.12 = 0.58
Q3. Let A and B be independent events with P (A) = 0.3 and P(B) = 0.4.Find P (A|B)
Answer : Option C
Explaination / Solution:
Let A and B be independent events with P (A) = 0.3 and P(B) = 0.4 P(A/B)=P(A)=0.3.
Q4. Let A and B be independent events with P (A) = 0.3 and P(B) = 0.4. Find P(B|A).
Answer : Option A
Explaination / Solution:
Let A and B be independent events with P (A) = 0.3 and P(B) = 0.4. P(B/A)=P(B)=0.4
Q5. If A and B are two events such that P(A) = ¼ , P(B) = ½ and , Find P(not A and not B ) .
Answer : Option A
Explaination / Solution:
Since A and B are independent events .
not A and not B are also independent events .
not A and not B are also independent events .
Q6. If A and B are two events such that A ⊂ B and P(B) ≠ 0, then which of the following is correct?
Answer : Option A
Explaination / Solution:
since A⊂B A⋂B=AP(A/B)=P(A⋂B)P(B)=P(A)P(B)
Q7. The probability of obtaining an even prime number on each die , when a pair of dice is rolled, is given by :
Answer : Option A
Explaination / Solution:
Clearly , n(s) =36. Favourable cases are { 2, 2 } Therefore required probability = 1/36 .
Q8. A bag contains 4 red and 4 black balls, another bag contains 2 red and 6 black balls. One of the two bags is selected at random and a ball is drawn from the bag which is found to be red. Find the probability that the ball is drawn from the first bag.
Answer : Option A
Explaination / Solution:


Q9.
Answer : Option D
Explaination / Solution:
Let are events of selection of a hostlier and a day scholar respectively.
Let A = event of getting grade A.
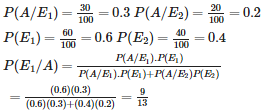
Let A = event of getting grade A.
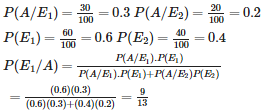
Q10. In answering a question on a multiple choice test, a student either knows the answer or guesses. Let be the probability that he knows the answer and be the probability that he guesses. Assuming that a student who guesses at the answer will be correct with probability . What is the probability that the student knows the answer given that he answered it correctly?
Answer : Option B
Explaination / Solution:
Let are events that the student knows the answer and the student guesses respectively.


