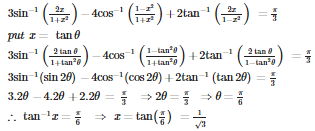CBSE 12TH MATHEMATICS - Online Test
Q1. For a real number x, let [x] denote the greatest integer less than or equal to x thenf (x) = is
Answer : Option B
Explaination / Solution:
Since [x−π] is an integer for all x∈R and tan nπ = 0 for all n∈I, therefore, F(x)= 0 for all x∈R.. So, f (X) is a constant and hence derivatives of f(x) of all order exist.
Q2.
The feasible region for a LPP is shown in Figure. Find the minimum value of Z = 11x + 7y.
Answer : Option C
Explaination / Solution:
Corner points | Z = 11x +7 y |
(0, 5 ) | 35 |
(0,3) | 21…………………(min.) |
(3,2 ) | 47 |
Hence the minimum value is 21
Q3. The domain of the function is
Answer : Option D
Explaination / Solution:
domain of the function is equals to {x R : g (x) ≠ 0 } = R – { x R : g (x) = 0 }.
Q4.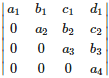 
is equal to
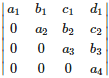is equal to
Answer : Option A
Explaination / Solution:
The determinant of a lower triangular or an upper triangular matrix is equal to the product of the diagonal elements.
Q6. If then f (x) – f (- x) is equal to
Answer : Option A
Explaination / Solution:
f(x)=|x|x=xx=1f(−x)=|−x|−x=x−x=−1f(x)−f(−x)=1−(−1)=1+1=2
Q7. Two cards are drawn at random and without replacement from a pack of 52 playing cards. Find the probability that both the cards are black.
Answer : Option D
Explaination / Solution:
Required probability : P(BB) = P(B) X P(B/B) ……………{B means black card} .
Q8. A box of oranges is inspected by examining three randomly selected oranges drawn without replacement. If all the three oranges are good, the box is approved for sale, otherwise, it is rejected. Find the probability that a box containing 15 oranges out of which 12 are good and 3 are bad ones will be approved for sale.
Answer : Option D
Explaination / Solution:
Total oranges = 15., Good Oranges = 12. Therefore , Required Probability =.
Q9.
Given that the events A and B are such that P(A) =, P (A ∪ B) = and P(B) = p. Find p if A and B are mutually exclusive
Answer : Option A
Explaination / Solution:
Since A and B are mutually exclusive events.,
Q10.
Given that the events A and B are such that P(A) =, P (A ∪ B) = and P(B) = p. Find p if they independent.
Answer : Option D
Explaination / Solution:
